题目内容
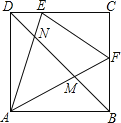
【题目】已知：如图，矩形ABCD的对角线AC的垂直平分线EF与AD、AC、BC分别交于点E、O、F．
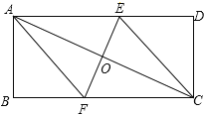
（1）求证：四边形AFCE是菱形；
（2）若AB=5，BC=12，EF=6，求菱形AFCE的面积．
【答案】（1）略；（2）39.
【解析】
（1）根据ASA证明△AOE≌△COF，得EO=FO，从而得出四边形AFCE为平行四边形，进一步由FE⊥AC，即可证得结论；
（2）根据勾股定理可求出AC的长，再根据菱形的面积公式即可求得结果.
解：（1）∵四边形ABCD是矩形，
∴AE∥FC，
∴∠EAO=∠FCO，
∵EF垂直平分AC，
∴AO=CO，FE⊥AC，
又∠AOE=∠COF，
∴△AOE≌△COF，
∴EO=FO，
∴四边形AFCE为平行四边形，
又∵FE⊥AC，
∴平行四边形AFCE为菱形；
（2）在Rt△ABC中，根据勾股定理得：
，又EF=6，∴菱形AFCE的面积
.
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
