Question

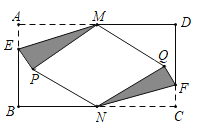
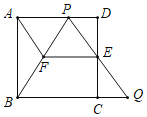
【题目】如图，在边长为l的正方形ABCD中，E是边CD的中点，点P是边AD上一点（与点A、D不重合），射线PE与BC的延长线交于点Q．

（1）求证：；

（2）过点E作交PB于点F，连结AF，当时，①求证：四边形AFEP是平行四边形；

②请判断四边形AFEP是否为菱形，并说明理由．

Answer 1

【答案】（1）见解析；（2）①见解析；②当时，四边形AFEP是菱形

【解析】

（1）由四边形ABCD是正方形知，由E是CD的中点知，结合即可得证；

（2）①由知，结合得，由知，再由知，根据中知，从而得，据此即可证得，从而得证；

②设，则，若四边形AFEP是菱形，则，由得关于x的方程，解之求得x的值，从而得出四边形AFEP为菱形的情况．

解：（1）四边形ABCD是正方形，

，

E是CD的中点，

，

又，

；

（2）①，

，

，

，

，

，

，

，

在中，，

，

，

，

，

四边形AFEP是平行四边形；

②当时，四边形AFEP是菱形．

设，则，

若四边形AFEP是菱形，则，

，E是CD中点，

，

在中，由得，

解得，

即当时，四边形AFEP是菱形．