Question

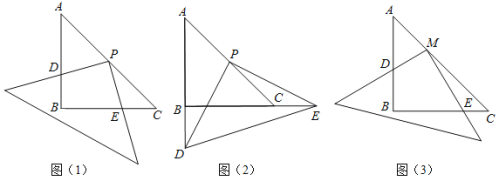
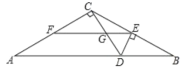
【题目】如图，正方形ABCD的边长为2，点E，F分别是DC和BC两边上的动点且始终保持∠EAF=45°，连接AE与AF交DB于点N，M．下列结论：①△ADM∽△NBA；②△CEF的周长始终保持不变其值是4；③AE×AM=AF×AN；④DN2+BM2=NM2．其中正确的结论是（　　）

A. ①②③B. ①②④C. ②③④D. ①③④

Answer 1

【答案】B

【解析】

①根据题意证明∠ANB=∠MAD，又因为∠ADM=∠ABN=45°，由AA证明△ADM∽△NBA；
②把△ADE顺时针旋转90°得到△ABG，证明△AEF≌△AGF，得到DG=EF，求出△CEF的周长；
③根据平行线的性质判断即可；
④把△ADN顺时针旋转90°得到△ABH，证明△NAM≌△HAM，根据勾股定理证明结论．

解：①∠ANB=∠NDA+∠NAD=45°+∠NAD，∠MAD=∠MAN+∠NAD=45°+∠NAD，
∴∠ANB=∠MAD，又∠ADM=∠ABN=45°，
∴△ADM∽△NBA，①正确；

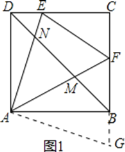
②如图1，把△ADE顺时针旋转90°得到△ABG，则BG=DE，∠FAG=∠FAB+∠DAE=45°，
在△AEF和△AGF中，
，
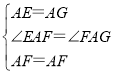∴△AEF≌△AGF，
∴FG=EF，
∴△CEF的周长=CE+CF+EF=CE+DE+CF+FB=4，②正确；
③当MN∥EF时，AE×AM=AF×AN，
∵MN与EF的位置关系不确定，∴③错误；

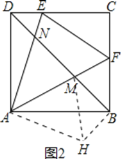
④如图2，把△ADN顺时针旋转90°得到△ABH，则BH=DN，∠ABH=∠AND=45°，∠MAH=∠MAB+∠BAH=∠MAB+∠DAN=45°，
在△NAM和△HAM中，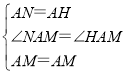
，
∴△NAM≌△HAM，
∴MN=MH，
又∵∠MBH=∠MBA+∠ABH=90°，
∴BH2+BM2=MH2，即DN2+BM2=NM2，④正确．
故选：B．