题目内容
【题目】如图，已知抛物线y＝ax2+bx+c经过A（﹣1，0）、B（5，0）、C（0，﹣5）三点．
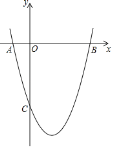
（1）求抛物线的解析式和顶点坐标；
（2）当0＜x＜5时，y的取值范围为 ；
（3）点P为抛物线上一点，若S△PAB＝21，直接写出点P的坐标．
【答案】（1）y＝（x﹣2）2﹣9，顶点坐标是（2，﹣9）；（2）﹣9≤y＜0；（3）（﹣2，7）或（6，7）或（
+2，﹣7）或（﹣+2，﹣7）
【解析】
（1）设抛物线的解析式为y＝a（x＋1）（x5），再将C（0，5）代入求出a的值，即可得到该抛物线的解析式；利用配方法将一般式化为顶点式，即可求出该抛物线的顶点坐标；
（2）根据图象即可求解；
（3）设点P的坐标为（x，y）．由S△PAB＝21，可得y＝±7．把y＝7与y＝7分别代入y＝x24x5，求出x的值，即可得到点P的坐标．
解：（1）设抛物线的解析式为y＝a（x+1）（x﹣5），
将C（0，﹣5）代入，得﹣5＝﹣5a，解得a＝1，
则该抛物线的解析式为y＝（x+1）（x﹣5），即y＝x2﹣4x﹣5；
∵y＝x2﹣4x﹣5＝（x﹣2）2﹣9，
∴该抛物线的顶点坐标是（2，﹣9）
（2）由图可得，当0＜x＜5时，﹣9≤y＜0．
故答案为﹣9≤y＜0；
（3）设点P的坐标为（x，y）．
∵A（﹣1，0）、B（5，0），
∴AB＝6．
∵S△PAB＝21，
∴
×6×|y|＝21，
∴|y|＝7，
∴y＝±7．
①当y＝7时，x2﹣4x﹣5＝7，解得x1＝﹣2，x2＝6，此时点P的坐标为（﹣2，7）或（6，7）；
②当y＝﹣7时，x2﹣4x﹣5＝﹣7，解得x1＝+2，x2＝﹣+2，此时点P的坐标为（+2，﹣7）或（﹣+2，﹣7）；
综上所述，所求点P的坐标为（﹣2，7）或（6，7）或（+2，﹣7）或（﹣+2，﹣7）．
