��Ŀ����
����Ŀ�������������һ���߳�Ϊn��n��2�����������ε�������n�ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬 ��������α��ʷֵ������еĽ��������߶����ֱ��Ƕ����أ�
����̽����Ҫ�о���������⣬���Dz����ȴ��������֣������ҵ�һ�����
̽��һ����һ���߳�Ϊ2���������ε�������ƽ�֣����Ӹ����е㣬��������α��ʷֵ������еĽ��������߶����ֱ��Ƕ��٣�
��ͼ1�����ӱ߳�Ϊ2���������������ߵ��е㣬�������£�����1+2+3=6����㣮�߳�Ϊ1���������Σ���һ����1�����ڶ�����2��������1+2=3�����߶���Ϊ3��3=9�����߳�Ϊ2������������1�����߶���Ϊ3�����ܹ���3����1+2+1��=2����1+2+3��=12���߶Σ�

̽��������һ���߳�Ϊ3���������ε����������ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬��������α��ʷֵ������еĽ��������߶����ֱ��Ƕ��٣�
��ͼ2�����ӱ߳�Ϊ3���������������ߵĶ�Ӧ���ȷֵ㣬�������£�����1+2+3+4=10����㣮�߳�Ϊ1���������Σ���һ����1�����ڶ�����2������������3��������1+2+3=6�����߶���Ϊ3��6=18�����߳�Ϊ2������������1+2=3�����߶���Ϊ3��3=9�����߳�Ϊ3������������1�����߶���Ϊ3�����ܹ���3����1+2+3+1+2+1��=3����1+2+3+4��=30���߶Σ�
̽������
�����������ķ�����̽�����߳�Ϊ4���������ε��������ĵȷ֣�ͼ3�������Ӹ��߶�Ӧ�ĵȷֵ㣬�������α��ʷֵ������еĽ��������߶����ֱ��Ƕ��٣�
������ʾ��ͼ����д��̽�����̣�
��������
�����������ķ�����̽����һ���߳�Ϊn��n��2�����������ε�������n�ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬��������α��ʷֵ������еĽ��������߶����ֱ��Ƕ��٣���д��̽�����̣�
ʵ��Ӧ�ã�
��һ���߳�Ϊ30���������ε���������ʮ�ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬��������α��ʷֵ������еĽ��������߶����ֱ��Ƕ��٣�
���𰸡�̽������������Ϊ10�����߶���Ϊ60������������������Ϊ![]() �����߶���Ϊ
�����߶���Ϊ![]() ����ʵ��Ӧ�ã�������Ϊ465�����߶���Ϊ14880��
����ʵ��Ӧ�ã�������Ϊ465�����߶���Ϊ14880��
��������
̽����������̽��һ��̽�����ķ�����⼴�ɣ�
������������̽��һ��̽������̽�����Ĺ����ܽ���ɼ��ɣ�
ʵ��Ӧ�ã����ݡ������������ܽ�Ĺ�����⼴�ɣ�
�⣺̽��������ͼ3�У�
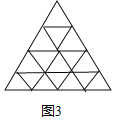
���ӱ߳�Ϊ4���������������ߵĶ�Ӧ�ĵȷֵ㣬�������£�����1+2+3+4+5=15����㣮�߳�Ϊ1���������Σ���һ����1�����ڶ�����2������������3�������IJ���4��������1+2+3+4=10�����߶���Ϊ3��10=30�����߳�Ϊ2������������1+2+3=6�����߶���Ϊ3��6=18�����߳�Ϊ3������������3�����߶���Ϊ3��3=9���߳�Ϊ4������������1�����߶���Ϊ3�����ܹ���3��(1+2+3+4+1+2+3+3+1)=4��(1+2+3+4+5)=60���߶Σ�
��������α��ʷֵ������еĽ�����Ϊ10�����߶���Ϊ60����
��������̽����һ���߳�Ϊn(n��2)���������ε�������n�ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬�������£�����1+2+3+4+5+��n=![]() ����㣮�߳�Ϊ1���������Σ���һ����1�����ڶ�����2������������3�������IJ���4������n����n��������(1+2+3+4+��+n)�����߶���Ϊ3��(1+2+3+4+��+n)�����߳�Ϊ2������������1+2+3=6�����߶���Ϊ3��6=18�����߳�Ϊ3������������3�����߶���Ϊ3��3=9���߳�Ϊ4������������1�����߶���Ϊ3�������߳�Ϊn��������1�����߶���Ϊ3���ܹ���n(1+2+3+��+n+1)=
����㣮�߳�Ϊ1���������Σ���һ����1�����ڶ�����2������������3�������IJ���4������n����n��������(1+2+3+4+��+n)�����߶���Ϊ3��(1+2+3+4+��+n)�����߳�Ϊ2������������1+2+3=6�����߶���Ϊ3��6=18�����߳�Ϊ3������������3�����߶���Ϊ3��3=9���߳�Ϊ4������������1�����߶���Ϊ3�������߳�Ϊn��������1�����߶���Ϊ3���ܹ���n(1+2+3+��+n+1)=![]() ��
��
��������α��ʷֵ������еĽ�����Ϊ![]() �����߶���Ϊ
�����߶���Ϊ![]() ����
����
ʵ��Ӧ�ã���һ���߳�Ϊ30���������ε���������ʮ�ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬��������α��ʷֵ������еĽ�����Ϊ![]() =465�����������߶�����=
=465�����������߶�����=![]() =14880���߶Σ�
=14880���߶Σ�
�������α��ʷֵ������еĽ�����Ϊ465�����߶���Ϊ14880����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ�������±��ش����⣺
x | 16 | 16.1 | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 |
x2 | 256 | 259.21 | 262.44 | 265.69 | 268.96 | 272.25 | 175.56 | 278.89 | 282.24 |
��1��272.25��ƽ������������������
��2��![]() =��������������
=�������������� ![]() =��������������
=�������������� ![]() =������������
=������������
��3����![]() ����������Ϊa����4a����������
����������Ϊa����4a����������