题目内容
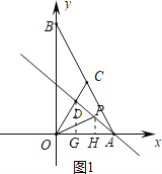
【题目】 如图,在平面直角坐标系中,点A和点B分别在x轴和y轴的正半轴上,OA=3,OB=2OA,C为直线y=2x与直线AB的交点,点D在线段OC上,OD=![]() .
.
(1)求点C的坐标;
(2)若P为线段AD上一动点(不与A、D重合).P的横坐标为x,△POD的面积为S,请求出S与x的函数关系式;
(3)若F为直线AB上一动点,E为x轴上一点,是否存在以O、D、E、F为顶点的四边形是平行四边形?若存在,写出点F的坐标;若不存在,请说明理由.

【答案】(1)点C坐标为(![]() ,3);(2)S =
,3);(2)S =![]() x-
x-![]() ;(3)存在,点F的坐标为(2,2)或(4,-2).
;(3)存在,点F的坐标为(2,2)或(4,-2).
【解析】
(1)根据题意求出A、B的坐标再求直线AB解析式,把直线AB与直线OC的方程联立方程组,求得的解即为点C坐标.
(2)由OD=![]() 及点D在直线y=2x上求得点D坐标,进而求得直线AD解析式,得到点P纵坐标的表示,用x表示△AOP的面积.利用S等于△AOD与△AOP面积差即求得S与x的函数关系式.
及点D在直线y=2x上求得点D坐标,进而求得直线AD解析式,得到点P纵坐标的表示,用x表示△AOP的面积.利用S等于△AOD与△AOP面积差即求得S与x的函数关系式.
(3)由于OD是固定的,所以以OD为平行四边形的边或对角线作为分类讨论的依据.画图即得到点F的纵坐标与点D纵坐标相等或互为相反数,把纵坐标代入直线AB解析式即求得F的横坐标.
解:(1)∵OA=3,点A和点B分别在x轴和y轴的正半轴上
∴A(3,0),OB=3OA=6
∴B(0,6)
设直线AB解析式为:y=kx+b
∴![]() 解得:
解得:![]()
∴直线AB解析式为:y=-2x+6
∵![]() 解得:
解得:![]()
∴点C坐标为(![]() ,3)
,3)
(2)过点D作DG⊥x轴于点G,过点P作PH⊥x轴于点H
∵点D在线段OC上,直线OC解析式为y=2x
∴设点D(d,2d)(0<d<![]() )
)
∴OD=![]()
∴d=1
∴D(1,2),DG=2
设直线AD解析式为:y=ax+c
∴![]() 解得:
解得:![]()
∴直线AD解析式为:y=-x+3
∵点P在线段AD上,且横坐标为x
∴OH=x,PH=yP=-x+3
∴S=S△AOD-S△AOP=![]() OADG-
OADG-![]() OAPH=
OAPH=![]() OA(DG-PH)=
OA(DG-PH)=![]() ×3×(2+x-3)=
×3×(2+x-3)=![]() x-
x-![]()
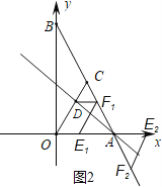
(3)存在以O、D、E、F为顶点的四边形是平行四边形.
①当OD为平行四边形的边时,如图2,
∴|yF|=yD=2
∵|-2x+6|=2解得:x1=2,x2=4
∴F(2,2)或(4,-2)
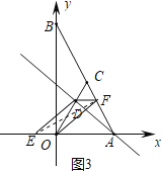
②当OD为平行四边形的对角线时,如图3,
∴DF∥x轴,yF=yD=2
∴F(2,2)
综上所述,点F的坐标为(2,2)或(4,-2).

 名校课堂系列答案
名校课堂系列答案