题目内容
【题目】如图,在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,连接AP. 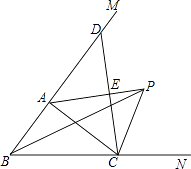
(1)求证:PA平分∠BAC的外角∠CAM;
(2)过点C作CE⊥AP,E是垂足,并延长CE交BM于点D.求证:CE=ED.
【答案】
(1)证明:
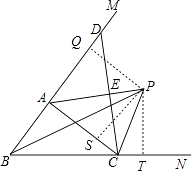
过P作PT⊥BC于T,PS⊥AC于S,PQ⊥BA于Q,如图,
∵在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,
∴PQ=PT,PS=PT,
∴PQ=PS,
∴AP平分∠DAC,
即PA平分∠BAC的外角∠CAM
(2)证明:∵PA平分∠BAC的外角∠CAM,
∴∠DAE=∠CAE,
∵CE⊥AP,
∴∠AED=∠AEC=90°,
在△AED和△AEC中
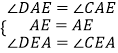
∴△AED≌△AEC,
∴CE=ED.
【解析】(1)过P作PT⊥BC于T,PS⊥AC于S,PQ⊥BA于Q,根据角平分线性质求出PQ=PS=PT,根据角平分线性质得出即可;(2)根据ASA求出△AED≌△AEC即可.
【考点精析】掌握角平分线的性质定理是解答本题的根本,需要知道定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.

练习册系列答案
相关题目