��Ŀ����
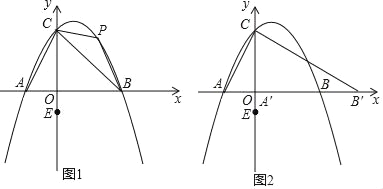
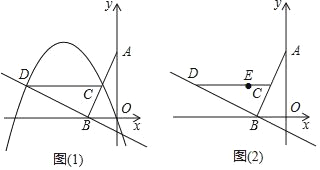
����Ŀ����֪������L��y��![]() x2+bx��2��x���ཻ��A��B���㣨��A�ڵ�B����ࣩ������y���ཻ�ڵ�C���ҵ�A�������ǣ���1��0����
x2+bx��2��x���ཻ��A��B���㣨��A�ڵ�B����ࣩ������y���ཻ�ڵ�C���ҵ�A�������ǣ���1��0����
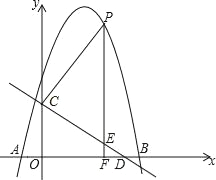
��1����������ߵĺ�������ʽ������D�����ꣻ
��2���ж���ABC����״���������ABC�������
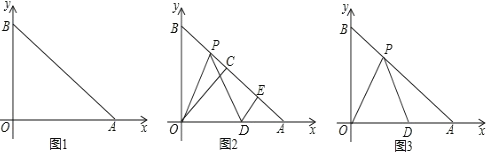
��3�������������������ƽ�ƣ��õ�������L�䣬L����x���ཻ��A'��B�����㣨��A���ڵ�B������ࣩ������y���ཻ�ڵ�C����Ҫʹ��A'B��C������ABC�������ȣ����������������������ߵĺ�������ʽ��

���𰸡�(1)y��![]() x2��
x2��![]() x��2������D��������
x��2������D��������![]() ����
����![]() ����(2)��ABC��ֱ�������Σ���ABC�������5��(3)�������������������ߵĺ�������ʽ��y��
����(2)��ABC��ֱ�������Σ���ABC�������5��(3)�������������������ߵĺ�������ʽ��y��![]() ��y��
��y��![]() ��y��
��y��![]() ��
��
��������
��1�����������߹���A������������ߵĽ���ʽ��Ȼ��������Ϊ����ʽ���ɵõ�����D�����ꣻ
��2�����ݣ�1���еĺ�������ʽ������õ�A��B��C�����꣬�Ӷ������ж���ABC����״��������������
��3������ƽ�Ƶ��ص�ͷ������۵ķ������������Ӧ�ĺ�������ʽ��
(1)��������L��y��![]() x2+bx��2����A����1��0����
x2+bx��2����A����1��0����
��0��![]() ������1��2+b������1����2��
������1��2+b������1����2��
��ã�b����![]() ��
��
��y��![]() x2��
x2��![]() x��2��
x��2��![]() ��
��
���D��������![]() ����
����![]() ����
����
���������ߵĺ�������ʽ��y��![]() x2��
x2��![]() x��2������D��������
x��2������D��������![]() ����
����![]() ����
����
(2)��y��0ʱ��0��![]() x2��
x2��![]() x��2����ã�x1����1��x2��4����x��0ʱ��y����2��
x��2����ã�x1����1��x2��4����x��0ʱ��y����2��
���A����1��0������B��4��0������C��0����2����
��AB��5��AC��![]() ��BC��2
��BC��2![]() ��
��
��AB2��AC2+BC2��
���ABC��ֱ�������Σ�
���ABC������ǣ�![]() ��5��
��5��
(3)�����������������ƽ�ƣ�
��ƽ�ƺ�A��B����ƽ��ǰ��AB�ij�����ȣ�
��ֻҪƽ�ƺ����0����2�������0��2��������������
������ƽ��ʱ��
��y��![]() ����x��0ʱ��y��
����x��0ʱ��y��![]() ��2����a��
��2����a��![]() ��
��
��ʱy��![]() ��
��![]() ��
��
������ƽ��ʱ��
��y��![]() ����x��0ʱ��y��
����x��0ʱ��y��![]() ����2����m��
����2����m��![]() ��m��3��
��m��3��
��m��![]() ʱ��y��
ʱ��y��![]() ����m��3ʱ��y��
����m��3ʱ��y��![]() ��2��
��2��
���Ͽɵã��������������������ߵĺ�������ʽ��y��![]() ��y��
��y��![]() ��y��
��y��![]() ��2��
��2��