Question

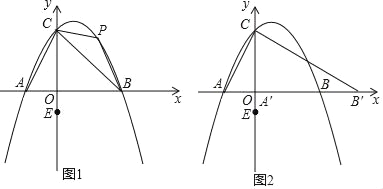
【题目】如图，在平面直角坐标系中，抛物线y＝﹣x2+x+2与x轴交于A、B两点，交y轴于点C，点C关于抛物线对称轴的对称点为点D．

(1)求线段AC的长度；

(2)P为线段BC上方抛物线上的任意一点，点E为（0，﹣1），一动点Q从点P出发运动到y轴上的点G，再沿y轴运动到点E．当四边形ABPC的面积最大时，求PG+GE的最小值；

(3)将线段AB沿x轴向右平移，设平移后的线段为A'B'，直至A'P平行于y轴（点P为第2小问中符合题意的P点），连接直线CB'．将△AOC绕着O旋转，设旋转后A、C的对应点分别为A'、C'，在旋转过程中直线A'C'与y轴交于点M，与线段CB'交于点N．当△CMN是以MN为腰的等腰三角形时，写出CM的长度．

Answer 1

【答案】(1)AC＝；(2)PG+GE的最小值为；(3)CM的长度为：2﹣或．

【解析】

（1）令y=0，则x=2或，令x=0，y=2，即：A（-，0）、B（2，0）、C（0，2），则AC=；

（2）过点P作y轴的平行线交BC于点H，设：P的横坐标为m，则P（m，-m2+m+2），H（m，-m+2），S四边形ABPC=S△ABC+S△PBC，S△ABC是个常量，∴四边形ABPC的面积最大时，只需要确定S△PBC最大即可，求出此时P（，2），过点E作RE⊥GR，使RE与y轴夹角为45度，则GR=GE，则：PG+GE=PG+GR，当P、G、R三点共线时，PG+GE有最小值即可求解；

（3）分MN=CM、MN=CN两种情况求解即可．

(1)令y＝0，则x＝2或，令x＝0，y＝2，即：A（﹣，0）、B（2，0）、C（0，2），

则AC＝，BC所在的直线方程为：y＝﹣x+2；

(2)过点P作y轴的平行线交BC于点H，

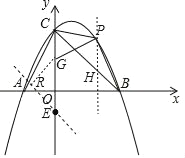
设：P的横坐标为m，则P（m，﹣m2+m+2），H（m，﹣m+2），

S四边形ABPC＝S△ABC+S△PBC，S△ABC是个常量，∴四边形ABPC的面积最大时，只需要确定S△PBC最大即可，

S△PBC即＝PH（xB）＝（﹣m2+m+2+m﹣2）＝（﹣m2+2m），

当m＝时，函数取得最大值，此时P（，2），

过点E作RE⊥GR，使RE与y轴夹角为45度，则GR＝GE，则：PG+GE＝PG+GR，

当P、G、R三点共线时，PG+GE有最小值，/span>

直线ER的方程为y＝﹣x﹣1…①，

则：直线PR方程的k值为1，其方程为：y＝x+…②，

联立①、②解得：R（﹣，），则：PR＝，

即PG+GE的最小值为；

(3)①当MN＝CM时，

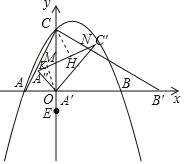
在等腰△MNC中，过C点作CH⊥MN，

设：MN＝CM＝a，CH＝x，tan∠MCN＝＝2，

由勾股定理得：a2＝x2+（a﹣）2，解得：x＝a，

则：tan∠CMH＝＝＝tan∠A″MA′，

在△A″MA′中，A′M＝CO﹣CM＝2﹣a，A′A″＝，tan∠C′A″A′＝2，

过点O作A′K⊥A″C′，则：A′K＝A′A″sinA″＝，AM＝，

则：CM＝2﹣；

②当MN＝CN时，过点N作NS⊥CM，

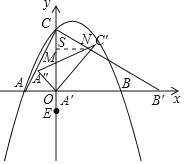
设N的横坐标为n，

∵tan∠MCN＝＝2，∴CS＝n，CM＝n，

∵∠MA″A′＝∠MCC′＝∠CMC′＝∠A′MA″，∴A′A″＝A′M＝2﹣n＝，

∴CM＝n＝；

故：CM的长度为：2﹣或．