题目内容
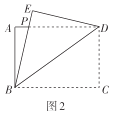
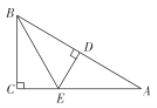
【题目】如图,在![]() ,
,![]() ,
,![]() ,作
,作![]() 的垂直平分线,交
的垂直平分线,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,则
,则![]() ( )
( )
A.2B.1C.![]() D.3
D.3
【答案】C
【解析】
首先利用直角三角形的性质求得∠ABC的度数,然后利用线段的垂直平分线的性质得到∠ABE的度数和AD的长度,从而求得BE平分∠ABC,从而利用角平分线的性质可得CE=DE,然后通过解直角三角形可求DE的长度,从而使问题得解.
解:∵△ABC中∠C=90°,∠A=30°,
∴∠ABC=60°,
∵AB的垂直平分线,交AB于D点,交AC于E点,
∴AE=BE,AD=BD=3
∴∠A=∠EBA=30°,
∴∠CBE=∠CBA-∠ABE=60°-30°=30°,
∴∠CBE=∠ABE
∴BE平分∠ABC
又因为∠C=90°,ED⊥AB
∴CE=DE
∴在Rt△ADE中,![]()
∴![]() ,即
,即![]() .
.
故选:C

练习册系列答案
相关题目