题目内容
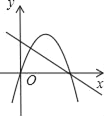
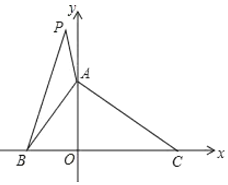
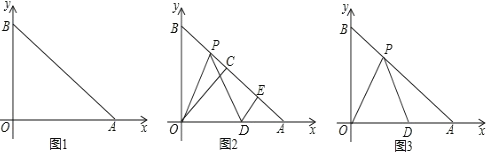
【题目】如图1在平面直角坐标系中,![]() 、
、![]() ,
,![]() 满足
满足![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 是线段
是线段![]() 上一动点,
上一动点,![]() 是
是![]() 轴正半轴上一点,且
轴正半轴上一点,且![]() ,
,![]() 于
于![]() .
.
(1)求![]() 的度数;
的度数;
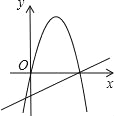
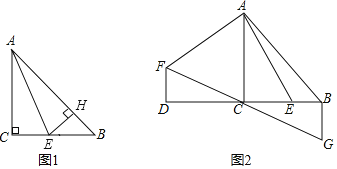
(2)如图2,设![]() ,当点
,当点![]() 运动时,
运动时,![]() 的值是否变化?若变化,说明理由;若不变,请求
的值是否变化?若变化,说明理由;若不变,请求![]() 的值;
的值;
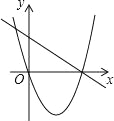
(3)如图3,设![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)∠OAB=45°;(2)PE的值不变.理由见解析;(3)D(6![]() 6,0).
6,0).
【解析】
(1)根据非负数的性质即可求得a,b的值,从而得到△AOB是等腰直角三角形,据此即可求得;
(2)根据等腰三角形的性质以及三角形的外角的性质可以得到∠POC=∠DPE,即可证得△POC≌△DPE,则OC=PE,OC的长度根据等腰直角三角形的性质可以求得;
(3)利用等腰三角形的性质,以及外角的性质证得∠POC=∠DPE,即可证得△POC≌△DPE,根据全等三角形的对应边相等,即可求得OD的长,从而求得D的坐标.
(1)根据题意得:
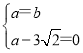 ,
,
解得:a=b=3![]() ,
,
∴OA=OB,
又∵∠AOB=90°
∴△AOB为等腰直角三角形,
∴∠OAB=45°.
(2)PE的值不变.理由如下:
∵△AOB为等腰直角三角形,且AC=BC,
∴∠AOC=∠BOC=45°
又∵OC⊥AB于C,
∵PO=PD
∴∠POD=∠PDO
当P在BC上时,
∵∠POD=45°+∠POC,∠PDO=45°+∠DPE,
∴∠POC=∠DPE
在△POC和△DPE中,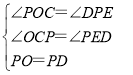 ,
,
∴△POC≌△DPE,
∴OC=PE
又OC=![]() AB=3
AB=3
∴PE=3;
当P在AC上时,∠POD=45°-∠POC,∠PDO=45°-∠DPE,
则∠POC=∠DPE.
同理可得PE=3;
(3)∵OP=PD,
∴∠POD=∠PDO=![]() =67.5°,
=67.5°,
则∠PDA=180°-∠PDO=180°-67.5°=112.5°,
∵∠POD=∠A+∠APD,
∴∠APD=67.5°-45°=22.5°,
∴∠BPO=180°-∠OPD-∠APD=112.5°,
∴∠PDA=∠BPO
则在△POB和△DPA中, ,
,
∴△POB≌△DPA(AAS).
∴PA=OB=3![]() ,
,
∴DA=PB=6-3![]() ,
,
∴OD=OA-DA=3![]() -(6-3
-(6-3![]() )=6
)=6![]() -6
-6
∴D(6![]() 6,0).
6,0).