题目内容
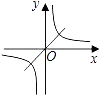
【题目】如图,在平面直角坐标系中,一次函数y=﹣ ![]() x+4的图象与x轴、y轴分别相交于点C、D,四边形ABCD是正方形,反比例函数y=
x+4的图象与x轴、y轴分别相交于点C、D,四边形ABCD是正方形,反比例函数y= ![]() 的图象在第一象限经过点A.
的图象在第一象限经过点A.
(1)求点A的坐标以及k的值:
(2)点P是反比例函数y= ![]() (x>0)的图象上一点,且△PAO的面积为21,求点P的坐标.
(x>0)的图象上一点,且△PAO的面积为21,求点P的坐标.
【答案】
(1)
解:由题可得:C(3,0),D(0,4).
过A作AE⊥y轴于E,如图(1):
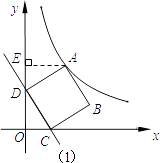
在△AED和△DOC中,  ,
,
∴△AED≌△DOC,
∴AE=DO=4,ED=OC=3,
∴A点坐标为(4,7),
∵点A在反比例函数y= ![]() 的图象上,
的图象上,
∴k=28
(2)
解:设点P坐标为(x, ![]() ),
),
①当点P在OA上方时,如图(2):

过P作PG⊥y轴于G,过A作AF⊥y轴于F,
∵S△APO+S△PGO=S四边形PGFA+S△AFO,S△PGO=S△AFO=14,
∴S△APO=S四边形PGFA,
有: ![]() (x+4)(
(x+4)( ![]() ﹣7)=21,
﹣7)=21,
解得:x1=﹣8(舍去),x2=2;
即点P的坐标为(2,14);
②当点P在OA下方时,如图(3):

过P作PH⊥x轴于H,过A作AM⊥x轴于M,
∵S△APO+S△PHO=S四边形PHMA+S△AMO,S△PHO=S△AMO=14,
∴S△APO=S四边形PHMA,
有: ![]() (
( ![]() +7)(x﹣4)=21,
+7)(x﹣4)=21,
解得:x3=﹣2(舍去),x4=8,
即点P坐标为(8, ![]() ).
).
综上可知:当点P坐标为(2,14)或(8, ![]() )时,△PAO的面积为21
)时,△PAO的面积为21
【解析】(1)过点A作AE⊥y轴于E,证明△AED≌△DOC,可得点A坐标,代入求解即可;(2)分两种情况讨论:①点P在OA上方时,过P作PG⊥y轴于G,过A作AF⊥y轴于F,通过得出S△APO=S四边形PGFA , 可得点P坐标;②点P在OA下方时,过P作PH⊥x轴于H,过A作AM⊥x轴于M,通过S△APO=S四边形PHMA , 可得点P坐标.
【考点精析】掌握反比例函数的概念和反比例函数的图象是解答本题的根本,需要知道形如y=k/x(k为常数,k≠0)的函数称为反比例函数.自变量x的取值范围是x不等于0的一切实数,函数的取值范围也是一切非零实数;反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案