题目内容
【题目】如图1在正方形ABCD的外侧作两个等边三角形ADE和DCF,连接AF,BE.
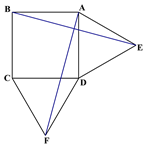
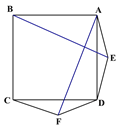

(图1) (图2) (备用图)
(1)请判断:AF与BE的数量关系是_____________,位置关系______________;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
【答案】(1)AF=BE,AF⊥BE(2)结论成立(3)结论都能成立
【解析】试题分析:(1)根据正方形和等边三角形可证明△ABE≌△DAF,然后可得BE=AF,∠ABE=∠DAF,进而通过直角可证得BE⊥AF;
(2)类似(1)的证法,证明△ABE≌△DAF,然后可得AF=BE,AF⊥BE,因此结论还成立;
(3)类似(1)(2)证法,先证△AED≌△DFC,然后再证△ABE≌△DAF,因此可得证结论.
试题解析:解:(1)AF=BE,AF⊥BE.
(2)结论成立.
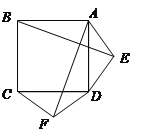
证明:∵四边形ABCD是正方形,
∴BA="AD" =DC,∠BAD =∠ADC = 90°.
在△EAD和△FDC中,
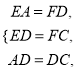
∴△EAD≌△FDC.
∴∠EAD=∠FDC.
∴∠EAD+∠DAB=∠FDC+∠CDA,
即∠BAE=∠ADF.
在△BAE和△ADF中,
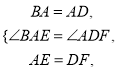
∴△BAE≌△ADF.
∴BE = AF,∠ABE=∠DAF.
∵∠DAF +∠BAF=90°,
∴∠ABE +∠BAF=90°,
∴AF⊥BE.
(3)结论都能成立.

练习册系列答案
相关题目