题目内容
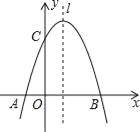
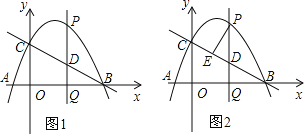
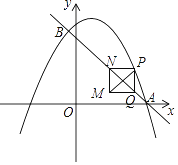
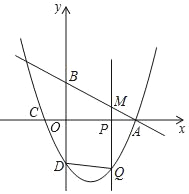
【题目】如图，在平面直角坐标系中，直线y＝﹣
x+2分别交x轴、y轴于点A、B．点C的坐标是（﹣1，0），抛物线y＝ax2+bx﹣2经过A、C两点且交y轴于点D．点P为x轴上一点，过点P作x轴的垂线交直线AB于点M，交抛物线于点Q，连结DQ，设点P的横坐标为m（m≠0）．
（1）求点A的坐标．
（2）求抛物线的表达式．
（3）当以B、D、Q，M为顶点的四边形是平行四边形时，求m的值．
【答案】（1）点A坐标为（4，0）；（2）y＝
x2﹣
x﹣2；（3）m＝2或1+
或1﹣．
【解析】
(1)直线y=﹣x+2中令y=0，即可求得A 点坐标；
(2)将A、C坐标代入，利用待定系数法进行求解即可；
(3)先求出BD的长，用含m的式子表示出MQ的长，然后根据BD=QM，得到关于m的方程，求解即可得.
(1)令y＝﹣x+2＝0，解得：x＝4，
所以点A坐标为：(4，0)；
(2)把点A、C坐标代入二次函数表达式，得
，
解得：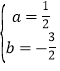
，
故：二次函数表达式为：y＝x2﹣x﹣2；
(3)y=﹣x+2中，令x=0，则y=2，故B(0，2)，
y＝x2﹣x﹣2中，令x=0，则y=-2，故D(0，-2)，
所以BD=4，
设点M(m，﹣m+2)，则Q(m，m2﹣m﹣2)，
则MQ=|(m2﹣m﹣2)-(﹣m+2)|=|m2﹣m﹣4|
以B、D、Q，M为顶点的四边形是平行四边形时，
则：|MQ|＝BD＝4，
即|m2﹣m﹣4|=4，
当m2﹣m﹣4=-4时，
解得：m＝2或m＝0(舍去)；
当m2﹣m﹣4=4时，
解得m＝1±，
故：m＝2或1+或1-．
练习册系列答案
相关题目
