题目内容
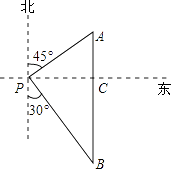
【题目】如图,已知直线![]() ,点
,点![]() 在直线
在直线![]() 上,点
上,点![]() 到直线
到直线![]() 的距离分别为1,2.
的距离分别为1,2.
(1)利用直尺和圆规作出以![]() 为底的等腰△ABC,使点
为底的等腰△ABC,使点![]() 在直线
在直线![]() 上(保留作图痕迹,不写作法).
上(保留作图痕迹,不写作法).
(2)若(1)中得到的△ABC为等腰直角三角形,求△ABC的面积.

【答案】(1)见解析(2)5
【解析】
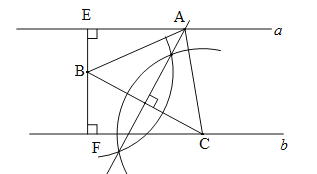
(1)作出线段BC的垂直平分线交直线a于点A,连结AB,AC,则△ABC即为所求;
(2)过点C作CD⊥a于D,根据同角的余角相等求出∠BAE=∠ACD,然后利用“角角边”证明△ABE≌△CAD,根据全等三角形对应边相等可得AE=CD,BE=AD,再利用勾股定理列式求出AC的长,然后根据等腰直角三角形的性质即可得出结论.
(1)如图所示:△ABC即为所求.
(2)如图,过点C作CD⊥a于D,则∠ACD+∠CAD=90°.
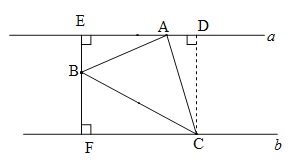
∵△ABC为等腰直角三角形,∴∠BAE+∠CAD=180°﹣90°=90°,∴∠BAE=∠ACD.
在△ABE和△CAD中,∵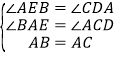 ,∴△ABE≌△CAD(AAS),∴AE=CD,BE=AD.
,∴△ABE≌△CAD(AAS),∴AE=CD,BE=AD.
∵BE=1,BF=2,∴AD=1,AE=CD=1+2=3.在Rt△ACD中,AC=![]() =
=![]() .
.
∵△ABC是等腰直角三角形,∴![]() =5.
=5.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案【题目】骑共享单车已成为人们喜爱的一种绿色出行方式.已知A、B、C三家公司的共享单车都是按骑车时间收费,标准如下:
公司 | 单价(元/半小时) | 充值优惠 |
A | m | 充20元送5元,即:充20元实得25元 |
B | m-0.2 | 无 |
C | 1 | 充20元送20元,即:充20元实得40元 |
(注:使用这三家公司的共享单车,不足半小时均按半小时计费.用户的账户余额长期有效,但不可提现.)
4月初,李明注册成了A公司的用户,张红注册成了B公司的用户,并且两人在各自账户上分别充值20元.一个月下来,李明、张红两人使用单车的次数恰好相同,且每次都在半小时以内,结果到月底李明、张红的账户余额分别显示为5元、8元.
(1)求m的值;
(2)5月份,C公司在原标准的基础上又推出新优惠:每月的月初给用户送出5张免费使用券(1
次用车只能使用1张券).如果王磊每月使用单车的次数相同,且在30次以内,每次用车都不超过
半小时. 若要在这三家公司中选择一家并充值20元,仅从资费角度考虑,请你帮他作出选择,并说
明理由.