题目内容
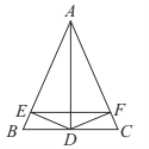
【题目】如图,△ABC中,AB的垂直平分线分别交AB,BC于D,E,AC的垂直平分线分别交AC,BC于F,G.
(1)若△AEG的周长为10,求线段BC的长.
(2)若∠BAC=128°,求∠EAG的度数.

【答案】(1)10;(2)76°
【解析】
(1)根据线段的垂直平分线的性质得到EB=EA,GA=GC,根据三角形的周长公式计算即可;
(2)根据三角形内角和定理求出∠B+∠C,再由等腰三角形的性质得到∠BAE=∠B,∠GAC=∠C,然后根据角的和差关系即可得出结论.
(1)∵DE是AB的垂直平分线,GF是AC的垂直平分线,∴EB=EA,GA=GC.
∵BC= BE+EG+GC,∴BC= AE+EG+AG=△AEG的周长=10.
(2)∵∠BAC=128°,∴∠B+∠C=180°-∠BAC=180°-128°=52°.
∵EB=EA,GA=GC,∴∠BAE=∠B,∠GAC=∠C,∴∠EAG=∠BAC-∠BAE-∠GAC=∠BAC-(∠B+∠C)=128°-52°=76°.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目