题目内容
【题目】绿色无公害蔬菜基地有甲、乙两种植户,他们种植了![]() 两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植 | 种植 | 总收入(单位:元) |
甲 |
|
|
|
乙 |
|
|
|
说明:不同种植户种植的同类蔬菜每亩的平均收入相等;亩为土地面积单位
![]() 求
求![]() 两类蔬菜每亩的平均收入各是多少元?
两类蔬菜每亩的平均收入各是多少元?
![]() 某种植户准备租
某种植户准备租![]() 亩地用来种植
亩地用来种植![]() 两类蔬菜,为了使总收入不低于
两类蔬菜,为了使总收入不低于![]() 元且种植
元且种植![]() 类蔬菜的面积多于种植
类蔬菜的面积多于种植![]() 类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案;
类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案;
![]() 在
在![]() 的基础上,指出哪种方案使总收入最大,并求出最大值.
的基础上,指出哪种方案使总收入最大,并求出最大值.
【答案】(1)![]() 两类蔬菜每亩平均收入分别是
两类蔬菜每亩平均收入分别是![]() 元,
元,![]() 元;(2)租地方案有4种,具体方案详见解析;(3)种植
元;(2)租地方案有4种,具体方案详见解析;(3)种植![]() 类蔬菜的面积为11亩,种植
类蔬菜的面积为11亩,种植![]() 类蔬菜的面积为9亩时,总收入最大,最大值为64500元.
类蔬菜的面积为9亩时,总收入最大,最大值为64500元.
【解析】
(1)设![]() 两类蔬菜每亩平均收入分别是
两类蔬菜每亩平均收入分别是![]() 元,
元,![]() 元,再根据甲、乙种植户的总收入建立二元一次方程组,然后解方程组即可;
元,再根据甲、乙种植户的总收入建立二元一次方程组,然后解方程组即可;
(2)结合(1)的结论,建立不等式组,然后求出其正整数解即可;
(3)设总收入为![]() 元,根据题(2)可得
元,根据题(2)可得![]() 与a的函数关系式,再根据一次函数的性质求解即可.
与a的函数关系式,再根据一次函数的性质求解即可.
(1)设![]() 两类蔬菜每亩平均收入分别是
两类蔬菜每亩平均收入分别是![]() 元,
元,![]() 元
元
由题意得:![]()
解得![]()
答:![]() 两类蔬菜每亩平均收入分别是
两类蔬菜每亩平均收入分别是![]() 元,
元,![]() 元;
元;
(2)设用来种植![]() 类蔬菜的面积
类蔬菜的面积![]() 亩,则用来种植
亩,则用来种植![]() 类蔬菜的面积为
类蔬菜的面积为![]() 亩,其中a为整数
亩,其中a为整数
由题意得: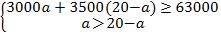
解得![]()
![]() 为整数
为整数
![]() a的取值为
a的取值为![]()
因此,租地方案有以下4个:
类别 | 种植面积单位: (亩) | |||
|
|
|
|
|
B |
|
|
|
|
(3)设总收入为![]() 元
元
由(2)可得:![]()
由一次函数的性质可知,当![]() 时,
时,![]() 随a的增大而减小
随a的增大而减小
则(2)中的4个方案中,当![]() 时,总收入
时,总收入![]() 最大,最大值为
最大,最大值为![]() (元)
(元)
答:种植![]() 类蔬菜的面积为11亩,种植
类蔬菜的面积为11亩,种植![]() 类蔬菜的面积为9亩时,总收入最大,最大值为64500元.
类蔬菜的面积为9亩时,总收入最大,最大值为64500元.

 阅读快车系列答案
阅读快车系列答案【题目】车间有20名工人,某天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
生产零件的个数(个) | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
工人人数(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求这一天20名工人生产零件的平均个数;
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
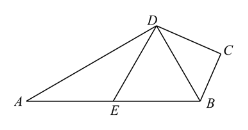
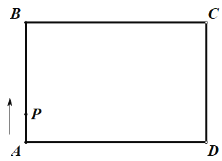
【题目】如图,在矩形![]() 中,
中,![]() 是
是![]() 延长线上的定点,
延长线上的定点,![]() 为
为![]() 边上的一个动点,连接
边上的一个动点,连接![]() ,将射线
,将射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,交射线
,交射线![]() 于点
于点![]() ,连接
,连接![]() .
.
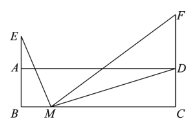
小东根据学习函数的经验,对线段![]() 的长度之间的关系进行了探究.
的长度之间的关系进行了探究.
下面是小东探究的过程,请补充完整:
(1)对于点![]() 在
在![]() 上的不同位置,画图、测量,得到了线段
上的不同位置,画图、测量,得到了线段![]() 的长度的几组值,如下表:
的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | |
| 0.00 | 0.53 | 1.00 | 1.69 | 2.17 | 2.96 | 3.46 | 3.79 | 4.00 |
| 0.00 | 1.00 | 1.74 | 2.49 | 2.69 | 2.21 | 1.14 | 0.00 | 1.00 |
| 4.12 | 3.61 | 3.16 | 2.52 | 2.09 | 1.44 | 1.14 | 1.02 | 1.00 |
在![]() 的长度这三个量中,确定_____的长度是自变量,_____的长度和_____的长度都是这个自变量的函数;
的长度这三个量中,确定_____的长度是自变量,_____的长度和_____的长度都是这个自变量的函数;
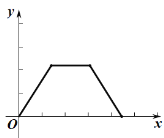
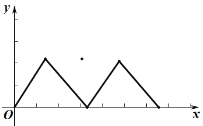
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的两个函数的图象;
中,画出(1)中所确定的两个函数的图象;
(3)结合画出的函数图象,解决问题:当![]() 时,
时,![]() 的长度约为________
的长度约为________![]() .
.