题目内容
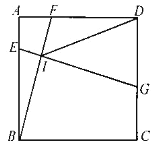
【题目】如图,四边形 ABCD 中,∠C=90°,AD⊥DB,点 E 为 AB 的中点,DE∥BC.
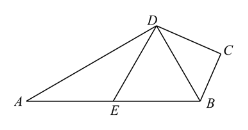
(1)求证:BD 平分∠ABC;
(2)连接 EC,若∠A =![]() ,DC=3,求 EC 的长.
,DC=3,求 EC 的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)直接利用直角三角形的性质得出DE=BE=![]() AB,再利用DE∥BC,得出∠2=∠3,进而得出答案;
AB,再利用DE∥BC,得出∠2=∠3,进而得出答案;
(2)利用已知得出在Rt△BCD中,∠3=60°,DC=3,解直角三角形得出DB的长,进而利用勾股定理得出EC的长.
(1)证明:∵AD⊥DB,点E为AB的中点,
∴DE=BE=![]() AB.
AB.
∴∠1=∠2.
∵DE∥BC,
∴∠2=∠3.
∴∠1=∠3.
∴BD平分∠ABC.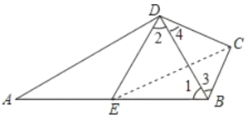
(2)解:∵AD⊥DB,∠A=30°,
∴∠1=60°.
∴∠3=∠2=60°.
∵∠BCD=90°,
∴∠4=30°.
∴∠CDE=∠2+∠4=90°.
在Rt△BCD中,∠3=60°,DC=3,
∴DB=![]() .
.
∵DE=BE,∠1=60°,
∴△BDE是等边三角形,
∴DE=DB=![]() .
.
∴EC=![]() .
.

 考前必练系列答案
考前必练系列答案【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
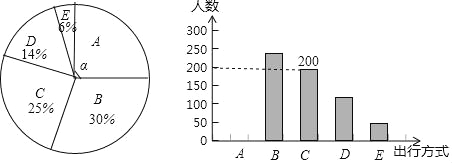
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
【题目】绿色无公害蔬菜基地有甲、乙两种植户,他们种植了![]() 两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植 | 种植 | 总收入(单位:元) |
甲 |
|
|
|
乙 |
|
|
|
说明:不同种植户种植的同类蔬菜每亩的平均收入相等;亩为土地面积单位
![]() 求
求![]() 两类蔬菜每亩的平均收入各是多少元?
两类蔬菜每亩的平均收入各是多少元?
![]() 某种植户准备租
某种植户准备租![]() 亩地用来种植
亩地用来种植![]() 两类蔬菜,为了使总收入不低于
两类蔬菜,为了使总收入不低于![]() 元且种植
元且种植![]() 类蔬菜的面积多于种植
类蔬菜的面积多于种植![]() 类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案;
类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案;
![]() 在
在![]() 的基础上,指出哪种方案使总收入最大,并求出最大值.
的基础上,指出哪种方案使总收入最大,并求出最大值.