Question

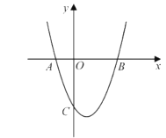
【题目】一种实验用轨道弹珠，在轨道上行驶5分钟后离开轨道，第一颗弹珠弹出后其速度（米/分钟）与时间（分钟）前2分钟满足二次函数，后3分钟满足反比例函数关系，如图，轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分钟．

（1）求第一颗弹珠的速度（米/分钟）与时间（分钟）之间的函数关系式；

（2）第一颗弹珠弹出1分钟后，弹出第二颗弹珠，第二颗弹珠的运行情况与第一颗相同，直接写出第二颗弹珠的速度（米/分钟）与弹出第一颗弹珠后的时间（分钟）之间的函数关系式；

（3）当两颗弹珠同时在轨道上时，第____分钟末两颗弹珠的速度相差最大，最大相差______；

（4）判断当两颗弹珠同时在轨道上时，是否存在某时刻速度相同？请说明理由，并指出可以通过解哪个方程求出这一时刻．

Answer 1

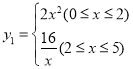【答案】（1）；（2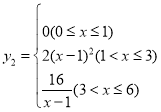）；（3）第2分钟末两颗弹珠速度相差最大，最大相差6米/分钟；（4）存在，理由详见解析

【解析】

（1）将（1，2）代入，得，从而得到，再代入求出，即可得到反比例函数解析式，即可得解；

（2）当时，第二颗弹珠未弹出，故第二颗弹珠的解析式为；再分别根据（1）中的结论，即可求出当和时第二颗弹珠的解析式；

（3）由图可知看出，前2分钟，弹珠的速度逐渐增大，则第2分钟末两颗弹珠速度相差最大，分别求出第2分钟末时两颗弹珠的速度，再相减即可的解；

（4）第2分钟末到第3分钟末，第一颗弹珠的速度由8米/分钟逐步下降到5米/分钟，第二颗弹珠的速度由2米/分逐步上升到8米/分，故在此期间必定存在一时刻，两颗弹珠的速度相同．可以根据速度相等时列方程求得时刻．

（1）当时，将（1，2）代入，得，

，

∵当时，，

∴当时，，

与的函数关系式为；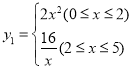

（2）当时，第二颗弹珠未弹出，

∴第二颗弹珠的解析式为；

当时，第二颗弹珠的解析式为；

当时，第二颗弹珠的解析式为；

∴与的函数关系式为；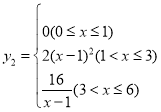

（3）由图可知看出，前2分钟，弹珠的速度逐渐增大，

∴第2分钟末两颗弹珠速度相差最大，

∵第一颗弹珠的速度为米/分钟，

第二颗弹珠的速度为米/分钟，

∴两颗弹珠的速度最大相差8-2=6米/分钟；

（4）存在，理由如下：

第2分钟末到第3分钟末，第一颗弹珠的速度由8米/分钟逐步下降到5米/分钟，

第二颗弹珠的速度由2米/分逐步上升到8米/分，

故在此期间必定存在一时刻，两颗弹珠的速度相同．

这个时刻可以通过解方程求得．