Question

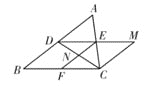
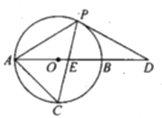
【题目】如图，在等腰中，，B是边AD上一点，以AB为直径的经过点P，C是上一动点，连接AC，PC，PC交AB于点E，且．

（1）求证：PD是的切线；

（2）连接OP，PB，BC，OC，若的直径是4，则：

①当四边形APBC是矩形时，求DE的长；

②当______时，四边形OPBC是菱形．

Answer 1

【答案】（1）见解析；（2）①；②3．

【解析】

（1）根据题意连接OP，运用等腰三角形的性质以及利用切线的定理即证明即可；

（2）①由题意可知PC是的直径，由（1）知，在中，，利用含60°的直角三角形的性质进行分析求解；

②根据题意利用菱形的性质即对角线互相垂直平分，以此进行分析即可.

解：（1）证明：如图1，连接OP.

∵，∴.

又∵，

∴.

∵，

∴，

∴.

又∵OP为半径，∴PD是的切线.

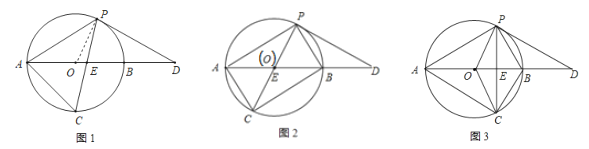
（2）解：①如图2，∵在矩形中，，

∴PC是的直径，

∴点与点E重合.

由（1）知，在中，.

又∵，

∴.

②如图3，∵四边形是菱形，∴PC，OB互相垂直平分，∴，∴.

∵，，∴.

故答案为：3.