题目内容
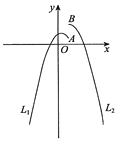
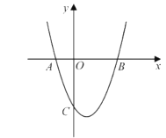
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() (
(![]() 在
在![]() 的左侧),交
的左侧),交![]() 轴于点
轴于点![]() ,且
,且![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)点![]() 为第四象限抛物线上一点,过点
为第四象限抛物线上一点,过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,设
,设![]() 点横坐标为
点横坐标为![]() ,线段
,线段![]() 的长度为
的长度为![]() ,求
,求![]() 与
与![]() 的函数关系式.(不要求写出
的函数关系式.(不要求写出![]() 的取值范围)
的取值范围)
(3)在(2)的条件下,![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)对于![]() ,令
,令![]() ,得
,得![]() ,从而点
,从而点![]() ,由
,由![]() 得到点
得到点![]() 将
将![]() 、
、![]() 代入
代入![]() ,由待定系数法即可抛物线的解析式为
,由待定系数法即可抛物线的解析式为![]() ;
;
(2)设![]() 由
由![]() ,
,![]() 可得直线
可得直线![]() 的解析式为
的解析式为![]() ,由
,由![]() 轴,故
轴,故![]() ,由此可得
,由此可得![]() ,从而
,从而![]() ;
;
(3)过点![]() 作
作![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,过点
,过点![]() 做
做![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() .由已知可得
.由已知可得![]() 、
、![]() 均为等腰直角三角形,从而
均为等腰直角三角形,从而![]() ,
,![]() ,由等式的性质可得
,由等式的性质可得![]() ,进而
,进而![]() ,由可得全等三角形的性质
,由可得全等三角形的性质![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() .由相似三角形的性质可得
.由相似三角形的性质可得![]() ,由三角形的面积可求得OM的值,在
,由三角形的面积可求得OM的值,在![]() 中,由正切的定义可求得t的值,由
中,由正切的定义可求得t的值,由![]() 即可得解.
即可得解.
(1)∵对于![]() ,
,
令![]() ,则
,则![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
将![]() 、
、![]() 代入
代入![]() ,
,
∴![]() ,解得,
,解得,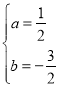
∴抛物线的解析式为![]() ;
;
(2)∵![]() 在抛物线
在抛物线![]() 上,设
上,设![]() ,
,
∵![]() ,
,![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
∵![]() 轴,
轴,
∴![]() 点的横坐标与
点的横坐标与![]() 点横坐标相同,
点横坐标相同,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
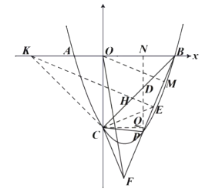
(3)过点![]() 作
作![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,过点
,过点![]() 做
做![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() .
.
∵![]() ,
,![]() ,
,
∴![]() 、
、![]() 均为等腰直角三角形,
均为等腰直角三角形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴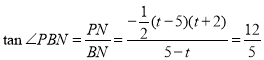 ,
,
∴![]() ,
,
∴![]()

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目