题目内容
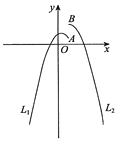
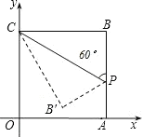
【题目】如图在平面直角坐标系中,四边形OABC是正方形,点A的坐标是(4,0),点p为边AB上的一点,![]() CPB=60°,沿CP折叠正方形后,点B落在平面内B’处,B’的坐标为( )
CPB=60°,沿CP折叠正方形后,点B落在平面内B’处,B’的坐标为( )
A.(2, 2![]() )B.(
)B.(![]() , 2-2
, 2-2![]() )C.(2, 4-2
)C.(2, 4-2![]() )D.(
)D.(![]() , 4-2
, 4-2![]() )
)
【答案】C
【解析】
作B′E⊥y轴于E,B′F⊥x轴于F,根据正方形的性质OC=BC=4,∠B=90°,由∠BPC=60°得∠1=30°,再根据折叠的性质得到∠1=∠2=30°,CB′=CB=4,所以∠3=30°,在Rt△CB′E中,根据含30度的直角三角形三边的关系得到B′E=![]() CB′=2,CE=
CB′=2,CE=![]() B′E=2
B′E=2![]() ,则OE=4-2
,则OE=4-2![]() ,所以B′F=4-2
,所以B′F=4-2![]() ,然后可写出B′点坐标.
,然后可写出B′点坐标.
解:作B′E⊥y轴于E,B′F⊥x轴于F,如图,

∵四边形OABC是正方形,点A的坐标是(4,0),
∴OC=BC=4,∠B=90°,
∵∠BPC=60°,
∴∠1=30°,
∵△CPB沿CP折叠,使得点B落在B′处,
∴∠1=∠2=30°,CB′=CB=4,
∴∠3=30°,
在Rt△CB′E中,B′E=![]() CB′=2,CE=
CB′=2,CE=![]() =2
=2![]() ,
,
∴OE=OC-CE=4-2![]() ,
,
∴B′F=OE=4-2![]() ,
,
∴B′点坐标为(2,4-2![]() ).
).
故选:C.

 阅读快车系列答案
阅读快车系列答案【题目】某公司的午餐采用自助的形式,并倡导员工“适度取餐,减少浪费”该公司共有10个部门,且各部门的人数相同.为了解午餐的浪费情况,从这10个部门中随机抽取了![]() 两个部门,进行了连续四周(20个工作日)的调查,得到这两个部门每天午餐浪费饭菜的重量,以下简称“每日餐余重量”(单位:千克),并对这些数据进行了整理、描述和分析.下面给出了部分信息.
两个部门,进行了连续四周(20个工作日)的调查,得到这两个部门每天午餐浪费饭菜的重量,以下简称“每日餐余重量”(单位:千克),并对这些数据进行了整理、描述和分析.下面给出了部分信息.![]() .
.![]() 部门每日餐余重量的频数分布直方图如下(数据分成6组:
部门每日餐余重量的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ):
):
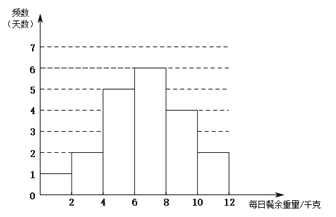
![]() .
.![]() 部门每日餐余重量在
部门每日餐余重量在![]() 这一组的是:6.1 6.6 7.0 7.0 7.0 7.8
这一组的是:6.1 6.6 7.0 7.0 7.0 7.8
![]() .
.![]() 部门每日餐余重量如下:1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
部门每日餐余重量如下:1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
![]() .
. ![]() 两个部门这20个工作日每日餐余重量的平均数、中位数、众数如下:
两个部门这20个工作日每日餐余重量的平均数、中位数、众数如下:
部门 | 平均数 | 中位数 | 众数 |
| 6.4 | | 7.0 |
| 6.6 | 7.2 | |
根据以上信息,回答下列问题:
(1)写出表![]() 中的值;
中的值;
(2)在![]() 这两个部门中,“适度取餐,减少浪费”做得较好的部门是________(填“
这两个部门中,“适度取餐,减少浪费”做得较好的部门是________(填“![]() ”或“
”或“![]() ”),理由是____________;
”),理由是____________;
(3)结合![]() 这两个部门每日餐余重量的数据,估计该公司(10个部门)一年(按240个工作日计算)的餐余总重量.
这两个部门每日餐余重量的数据,估计该公司(10个部门)一年(按240个工作日计算)的餐余总重量.