题目内容
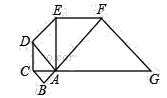
【题目】如图，已知△ABC是腰长为1的等腰直角三形，以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，…，依此类推，则第2018个等腰直角三角形的斜边长是______．
【答案】（
）2018
【解析】
首先根据△ABC是腰长为1的等腰直角三形，求出△ABC的斜边长是，然后根据以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，求出第2个等腰直角三角形的斜边长是多少；再根据以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，求出第3个等腰直角三角形的斜边长是多少，推出第2017个等腰直角三角形的斜边长是多少即可．
解：∵△ABC是腰长为1的等腰直角三形，
∴△ABC的斜边长是,
第2个等腰直角三角形的斜边长是：×=（）2，
第3个等腰直角三角形的斜边长是：（）2×=（）3，
…，
∴第2012个等腰直角三角形的斜边长是（）2018.
故答案为：（）2018.
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
【题目】二次函数y=ax2+bx+c（a、b、c为常数，且a≠0）中x与y的部分对应值如表：
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
①ac＜0；
②当x＞1时，y的值随x值的增大而减小；
③x=3是方程ax2+（b﹣1）x+c=0的一个根；
④当﹣1＜x＜3时，ax2+（b﹣1）x+c＞0．
上述结论中正确的个数是（ ）
A.4
B.3
C.2
D.1
