题目内容
(2013•松北区一模)哈市某中学计划创建中、小型两类班级图书角,已知组建一个中型图书角需科技类书籍80本,人文类书籍50本,共需购书费用860元;组建一个小型图书角需科技类书籍30本,人文类书籍60本,共需购书费用570元,又知每本科技类书籍价格相同,每本人文类书籍的价格也相同.
(1)求每本科技类书籍和每本人文类书籍的价格分别为多少元?
(2)若该学校计划用不超过20100元的资金组建中、小型两类图书角共30个,求最多组建多少个中型图书角?
(1)求每本科技类书籍和每本人文类书籍的价格分别为多少元?
(2)若该学校计划用不超过20100元的资金组建中、小型两类图书角共30个,求最多组建多少个中型图书角?
分析:(1)设每本科技类书籍的价格为x元,每本人文类书籍的价格为y元,根据题意建立方程求出其解就可以了;
(2)设可以组建m个中型图书角,则小型图书角为(30-m)个,根据题意建立不等式组就可以求出结论.
(2)设可以组建m个中型图书角,则小型图书角为(30-m)个,根据题意建立不等式组就可以求出结论.
解答:解:(1)设每本科技类书籍的价格为x元,每本人文类书籍的价格为y元,由题意得:
,
解得:
答:科技类每本7元,人文类每本6元
(2)设可以组建m个中型图书角,则小型图书角为(30-m)个,由题意得:
860m+570(30-m)≤20100,
解得:m≤
,
∵m为整数,
∴想的最大整数为:10
答:中型图书角最多10个.
|
解得:
|
答:科技类每本7元,人文类每本6元
(2)设可以组建m个中型图书角,则小型图书角为(30-m)个,由题意得:
860m+570(30-m)≤20100,
解得:m≤
| 300 |
| 29 |
∵m为整数,
∴想的最大整数为:10
答:中型图书角最多10个.
点评:本题考查了列二元一次方程组解决实际问题的运用及二元一次方程组的解法,列不等式解实际问题的运用及不等式的解法.解答时运用m为整数的条件求解m的最大值是关键.

练习册系列答案
相关题目
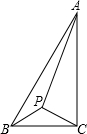 (2013•松北区一模)如图,P为△ABC内一点,∠BAC=30°,∠ACB=90°,∠BPC=120°.若BP=
(2013•松北区一模)如图,P为△ABC内一点,∠BAC=30°,∠ACB=90°,∠BPC=120°.若BP=