题目内容
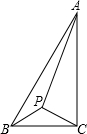（2013•松北区一模）如图，P为△ABC内一点，∠BAC=30°，∠ACB=90°，∠BPC=120°．若BP=| 3 |
3
| ||
| 2 |
3
| ||
| 2 |
分析：如图，作△BPC的外接圆⊙O，交AC的延长线于D，连接BD、PD．利用切线的性质和圆内接四边形的内对角互补得到∠BDA=180°-∠BPC=60°，所以∠ABD=180°-∠BAC-∠BDA=90°，即AB是⊙O的切线．设∠ABP=∠BDP=α．通过解直角△ABD、△BPD求得AB、AP的长度，然后由三角形的面积公式S=
absinC进行计算即可．
| 1 |
| 2 |
解答：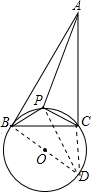
解：如图，作△BPC的外接圆⊙O，交AC的延长线于D，连接BD、PD．
∵∠ACB=90°，
∴∠BCD=90°，
∴BD是⊙O的直径．
∵四边形BDCP是圆内接四边形，
∴∠BDA=180°-∠BPC=60°，
∴∠ABD=180°-∠BAC-∠BDA=180°-30°-60°=90°，则AB是⊙O的切线．
设∠ABP=∠BDP=α．
在直角△ABD中，AB=BD•tan∠BDA=
BD，
在直角△BPD中，BP=BD•sin∠BDP=BDsinα=
，
则△PAB的面积是：
AB•BPsin∠ABP=
×
BD×
sinα=
．
解：如图，作△BPC的外接圆⊙O，交AC的延长线于D，连接BD、PD．∵∠ACB=90°，
∴∠BCD=90°，
∴BD是⊙O的直径．
∵四边形BDCP是圆内接四边形，
∴∠BDA=180°-∠BPC=60°，
∴∠ABD=180°-∠BAC-∠BDA=180°-30°-60°=90°，则AB是⊙O的切线．
设∠ABP=∠BDP=α．
在直角△ABD中，AB=BD•tan∠BDA=
| 3 |
在直角△BPD中，BP=BD•sin∠BDP=BDsinα=
| 3 |
则△PAB的面积是：
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
3
| ||
| 2 |
点评：本题考查了圆的综合题．其中涉及到了圆周角定理，圆内接四边形的性质，解直角三角形以及三角形的面积计算．此题的难点是作出△BPC的外接圆⊙O．
练习册系列答案
相关题目