题目内容
（2013•松北区一模）已知△ABC中，AC=BC=8，∠ACB=90°，D是直线AC上一点，CD：AC=1：2，折叠△ABC，使B落在D点上，则折痕长为
．
5
| ||
| 3 |
5
| ||
| 3 |
分析：根据CD：AC=1：2，即可求得CD的长，设BE=x，在△DCE中根据勾股定理求出x的值，故可得出△ABC，△CDE，△ADF的面积，进而得出四边形CEDF的面积，再根据S四边形CEDF=
BD•EF即可得出结论．
| 1 |
| 2 |
解答：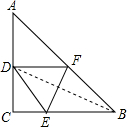
解：设折痕为EF，则BD为EF的垂直平分线，
∵CD：AC=1：2，
∴CD=
AC=4，
设BE=x，则在△DCE中，
（8-x）2+42=x2，解得x=5，即BE=DE=5，CE=3，
BF=
，AC=
，
∵S△ABC=32，S△CDE=6，S△ADF=
，
∴S四边形CEDF=
BD•EF=
=2
EF，解得EF=
．
解：设折痕为EF，则BD为EF的垂直平分线，∵CD：AC=1：2，
∴CD=
| 1 |
| 2 |
设BE=x，则在△DCE中，
（8-x）2+42=x2，解得x=5，即BE=DE=5，CE=3，
BF=
10
| ||
| 3 |
14
| ||
| 3 |
∵S△ABC=32，S△CDE=6，S△ADF=
| 28 |
| 5 |
∴S四边形CEDF=
| 1 |
| 2 |
| 50 |
| 3 |
| 5 |
5
| ||
| 3 |
点评：本题是相似三角形的判定与性质以及轴对称的性质的综合应用，根据轴对称的性质理解折痕EF是BD的中垂线是关键．
练习册系列答案
相关题目
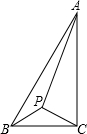（2013•松北区一模）如图，P为△ABC内一点，∠BAC=30°，∠ACB=90°，∠BPC=120°．若BP=