题目内容
(2013•松北区一模)小高从家门口骑车去离家4千米的单位上班,先花3分钟走平路1千米,再走上坡路以0.2千米/分钟的速度走了5分钟,最后走下坡路花了4分钟到达工作单位,若设他从家开始去单位的时间为t(分钟),离家的路程为y(千米),则y与t(8<t≤12)的函数关系为( )
分析:当8<t≤12时,小高正在走下坡路,求出走下坡路的速度,然后根据y=平路+上坡路+(t-8)×下坡路速度,即可得出答案.
解答:解:下坡路的长度=4-1-0.2×5=2千米,下坡路的速度=2÷4=0.5千米/分钟,
则y=平路+上坡路+(t-8)×下坡路速度=2+0.5×(t-8)=0.5t-2,
即可得y=0.5t-2(8<t≤12).
故选D.
则y=平路+上坡路+(t-8)×下坡路速度=2+0.5×(t-8)=0.5t-2,
即可得y=0.5t-2(8<t≤12).
故选D.
点评:本题考查了由实际问题抽象一次函数关系式的知识,解答本题的关键是求出走下坡路时的速度,难度一般.

练习册系列答案
相关题目
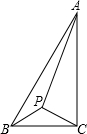 (2013•松北区一模)如图,P为△ABC内一点,∠BAC=30°,∠ACB=90°,∠BPC=120°.若BP=
(2013•松北区一模)如图,P为△ABC内一点,∠BAC=30°,∠ACB=90°,∠BPC=120°.若BP=