题目内容
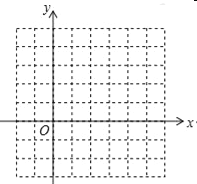
【题目】如图，在8×8网格纸中，每个小正方形的边长都为1．
（1）已知点A在第四象限，且到x轴距离为1，到y轴距离为5，求点A的坐标；
（2）在（1）的条件下，已知点B（a+1，﹣2a+10），且点B在第一、三象限的角平分线上，判断△OAB的形状．
【答案】(1)（5，﹣1）；(2)等腰三角形．
【解析】
试题分析：（1）根据第四象限的点的横坐标是正数，纵坐标是负数，点到x轴的距离等于纵坐标的长度，到y轴的距离等于横坐标的长度确定出点的横坐标与纵坐标，即可得解；
（2）根据第一、三象限角平分线上点的特点可知点B的坐标，根据勾股定理可求OB，AB，OA的长，再由勾股定理的逆定理即可得到△ABO是等腰三角形．
试题解析：（1）∵点在第四象限且到x轴距离为1，到y轴距离为5，
∴点的横坐标是5，纵坐标是﹣1，
∴点A的坐标为（5，﹣1）；
（2）∵点B（a+1，﹣2a+10）在第一、三象限的角平分线上，
∴a+1=﹣2a+10，
解得a=3；
∴点B的坐标是（4，4），
由勾股定理得
=32，
=26，
=26，
∴+≠，AB=OA，
∴△ABO是等腰三角形．
练习册系列答案
相关题目
