题目内容
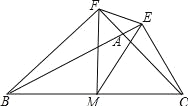
【题目】如图,在△ABC中,CE⊥BA的延长线于E,BF⊥CA的延长线于F,M为BC的中点,分别连接ME、MF、EF.
(1)若EF=3,BC=10,求△EFM的周长;
(2)若∠ABC=29°,∠ACB=46°,求∠EMF的度数.
【答案】(1)13;(2)30°.
【解析】
试题分析:(1)根据直角三角形斜边中线的性质得出EM=FM=![]() BC=5,进而可求得△EFM的周长;
BC=5,进而可求得△EFM的周长;
(2)根据直角三角形斜边中线的性质得出EM=BM,FM=MC,根据等腰三角形的性质和三角形内角和定理得出∠EMC=58°,∠FMC=88°,进而可求得∠FME=88°﹣58°=30°.
试题解析:(1)∵CE⊥BA,M为BC的中点,
∴EM=![]() BC=4,
BC=4,
∵BF⊥CA,M为BC的中点,
∴FM=![]() BC=4,
BC=4,
∴△EFM的周长为:EM+FM+EF=5+5+3=13;
(2)∵EM=![]() BC,M为BC的中点,
BC,M为BC的中点,
∴BM=EM,
∴∠EBM=∠BEM=29°,
∴∠EMC=58°,
∵FM=![]() BC,M为BC的中点,
BC,M为BC的中点,
∴FM=MC,
∴∠MFC=∠ACB=46°,
∴∠FMC=88°,
∴∠FME=88°﹣58°=30°.

练习册系列答案
相关题目
【题目】根据下列表格的对应值,判断ax2+bx+c=0 (a≠0,a,b,c为常数)的一个解x的取值范围是_____
x | 3.23 | 3.24 | 3.25 | 3.26 |
ax2+bx+c | ﹣0.06 | ﹣0.02 | 0.03 | 0.09 |