题目内容
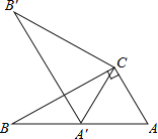
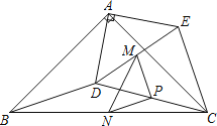
【题目】如图,△ABC,△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,将△ADE绕点A在平面内自由旋转,连接DC,点M,P,N分别为DE,DC,BC的中点,若AD=3,AB=7,则线段MN的取值范围是______.
【答案】2![]() ≤MN≤5
≤MN≤5![]()
【解析】
根据中位线定理和等腰直角三角形的判定证明△PMN是等腰直角三角形,求出MN=![]() BD,然后根据点D在AB上时,BD最小和点D在BA延长线上时,BD最大进行分析解答即可.
BD,然后根据点D在AB上时,BD最小和点D在BA延长线上时,BD最大进行分析解答即可.
∵点P,M分别是CD,DE的中点,
∴PM=![]() CE,PM∥CE,
CE,PM∥CE,
∵点P,N分别是DC,BC的中点,
∴PN=![]() BD,PN∥BD,
BD,PN∥BD,
∵△ABC,△ADE均为等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴PM=PN,
∴△PMN是等腰三角形,
∵PM∥CE,
∴∠DPM=∠DCE,
∵PN∥BD,
∴∠PNC=∠DBC,
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,
∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
∵∠BAC=90°,
∴∠ACB+∠ABC=90°,
∴∠MPN=90°,
∴△PMN是等腰直角三角形,
∴PM=PN=![]() BD,
BD,
∴MN=![]() BD,
BD,
∴点D在AB上时,BD最小,
∴BD=AB-AD=4,MN的最小值2![]() ;
;
点D在BA延长线上时,BD最大,
∴BD=AB+AD=10,MN的最大值为5![]() ,
,
∴线段MN的取值范围是2![]() ≤MN≤5
≤MN≤5![]() .
.
故答案为:2![]() ≤MN≤5
≤MN≤5![]() .
.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目