题目内容
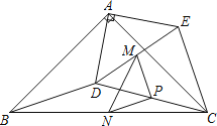
【题目】如图1已知抛物线y=ax2+bx﹣3与x轴相交于A(﹣1,0)、B(3,0),P为抛物线上第四象限上的点.
(1)求该抛物线的函数关系式;
(2)如图1,过点P作PD⊥x轴于点D,PD交BC于点E,当线段PE的长度最大时,求点P的坐标.
(3)如图2,当线段PE的长度最大时,作PF⊥BC于点F,连结DF.在射线PD上有一点Q,满足∠PQB=∠DFB,问在坐标轴上是否存在一点R,使得S△RBE=S△QBE?如果存在,直接写出R点的坐标;如果不存在,请说明理由.
【答案】(1)y=x2﹣2x﹣3;(2)当m=![]() 时,PE最大,此时P(
时,PE最大,此时P(![]() ,﹣
,﹣![]() );(3)R的坐标为:(﹣
);(3)R的坐标为:(﹣![]() ,0)或(
,0)或(![]() ,0)或(0,
,0)或(0,![]() )或(0,﹣
)或(0,﹣![]() ).
).
【解析】
(1)利用待定系数法求出抛物线解析式;
(2)首先求出点C的坐标,再由待定系数法求得直线BC的解析式是y=x﹣3;设P(m,m2﹣2m﹣3).过点P作PD⊥x轴于点D,PD交BC于点E,从而E(m,m﹣3),故PE=(m﹣3)﹣(m2﹣2m﹣3)=﹣m2+3m=﹣(m![]() )2
)2![]() ,从而求得当m
,从而求得当m![]() 时,PE最大,此时P(
时,PE最大,此时P(![]() );
);
(3)首先求得点E的坐标,PE长度,进而得出BD的长度,根据点B、C的坐标判断出△OBC是等腰直角三角形,进而根据勾股定理得到BE的长度,根据对顶角相等推知在直角△PEF中,∠PEF=90°,根据勾股定理得出EF的长度,从而求得BF的长度,然后判断出△QBE∽△FDB,由相似三角形的对应边成比例列出方程,求得QE的长度,根据三角形的面积公式求出S△BQE.当R点在x轴上时,设R(n,0),BR=|3﹣n|,根据S△RBE=S△QBE列出方程求得n的值,得出R点的坐标;当点R在y轴上时,设R(0,z),由S△BER=S△BRC﹣S△REC列出方程求得z的值,再求出R点在y轴上时的坐标,从而得出本题的答案.
(1)将A(﹣1,0)、B(3,0)分别代入y=ax2+bx﹣3得:![]() ,解得:
,解得:![]() ,所以该抛物线解析式为y=x2﹣2x﹣3;
,所以该抛物线解析式为y=x2﹣2x﹣3;
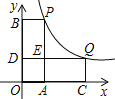
(2)如图1,把x=0代入y=x2﹣2x﹣3,得:y=﹣3,∴C(0,﹣3).
设直线BC的解析式为:y=kx+b,将C(0,﹣3)与B(3,0),分别代入得:![]() ,解得:
,解得:![]() ,∴直线BC的解析式为y=x﹣3.
,∴直线BC的解析式为y=x﹣3.
设P(m,m2﹣2m﹣3),则E(m,m﹣3),∴PE=(m﹣3)﹣(m2﹣2m﹣3)=﹣m2+3m=﹣(m![]() )2
)2![]() ,故当m
,故当m![]() 时,PE最大,此时P(
时,PE最大,此时P(![]() );
);
(3)如图2,当线段PE的长度最大时,P(![]() ),E(
),E(![]() ),PE
),PE![]() ,∴D(
,∴D(![]() ,0),∴BD
,0),∴BD![]() .
.
∵B(3,0),C(0,﹣3),∴OB=OC=3,∴△OBC是等腰直角三角形,∴∠OBC=45°.
在直角△DBE中,∠ABC=45°,BD![]() ,∴BE
,∴BE![]() ,∠DEB=45°,∴∠PEF=45°.
,∠DEB=45°,∴∠PEF=45°.
在直角△PEF中,∠PEF=45°,PE![]() ,∴EF
,∴EF![]() ,∴BF
,∴BF![]() .
.
∵∠PQB=∠DFB,∠DBE=∠DEB=45°,∴△QBE∽△FDB,∴![]() ,即
,即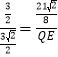 ,∴QE
,∴QE![]() .
.
∵S△BQE![]() QEDB
QEDB![]() .
.
当点R在x轴上时,设R(n,0),BR=|3﹣n|,∴S△RBE![]() BRDE,即
BRDE,即![]() |3﹣n|
|3﹣n|![]() ,则|3﹣n|
,则|3﹣n|![]() ,解得:n1
,解得:n1![]() ,n2
,n2![]() ,∴R(
,∴R(![]() ,0)或(
,0)或(![]() ,0)
,0)
当R在y轴上时,设R(0,z),由S△BER=S△BRC﹣S△REC得到:![]() 3×|z+3|
3×|z+3|![]() |z+3|
|z+3|
解得:z1![]() ,z2
,z2![]() ,∴R(0,
,∴R(0,![]() )或(0,
)或(0,![]() ).
).
综上所述:符合条件的点R的坐标为:(![]() ,0)或(
,0)或(![]() ,0)或(0,
,0)或(0,![]() )或(0,
)或(0,![]() ).
).

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案