题目内容
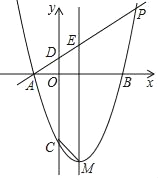
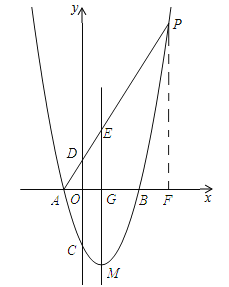
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c的对称轴为直线x=1,抛物线与x轴交于A、B两点(点A在点B的左侧),且AB=4,又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与对称轴交于点E,设点P的横坐标为t.
(1)求点A的坐标和抛物线的表达式;
(2)当AE:EP=1:2时,求点E的坐标;
(3)记抛物线的顶点为M,与y轴的交点为C,当四边形CDEM是等腰梯形时,求t的值.
【答案】(1)y=x2﹣2x﹣3;(2)E(1,4);(3)t=4.
【解析】分析:(1)依据抛物线的对称性可得到A、B的坐标,利用抛物线的交点式可得到抛物线的解析式;
(2)过点P作PF∥y轴,交x轴与点F,则△AEG∽△APF,从而可得到AF=6,然后可求得PF的长,从而可得到EG的长,故此可得到点E的坐标;
(3)先证明∠ADO=∠CME,然后,再求得点C和点M的坐标,从而可得到tan∠ADO=1,于是可得到OD=AO=1,故此可得到AP的解析式,最后求得直线AP与抛物线的交点坐标即可.
详解:(1)∵AB=4,抛物线y=x2+bx+c的对称轴为直线x=1,∴点A到对称轴的距离为2,∴A(﹣1,0),B(3,0),∴y=(x+1)(x﹣3)整理得:y=x2﹣2x﹣3;
(2)如下图所示:过点P作PF⊥x轴,垂足为F.
∵EG∥PF,AE:EP=1:2,∴![]() =
=![]() =
=![]() .
.
又∵AG=2,∴AF=6,∴F(5,0).
当x=5时,y=12,∴EG=4,∴E(1,4).
(3)∵CD∥EM,∴∠ADO=∠AEM.
又∵四边形CDEM是等腰梯形,∴∠ADO=∠CME,∴∠ADO=∠CME.
∵y=x2﹣2x﹣3,∴C(0,﹣3),M(1,﹣4)
∴tan∠DAO=tan∠CME=1,∴OA=OD=1,∴直线AP的解析式为y=x+1.
把y=x+1代入y=x2﹣2x﹣3得:x+1=x2﹣2x﹣3,解得:x=4或x=﹣1(舍去)
∴点P的横坐标为4,即t=4.

 名校课堂系列答案
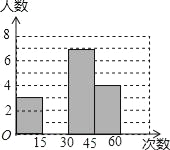
名校课堂系列答案【题目】在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分 组 | 频数 | 频率 |
第一组(0≤x<15) | 3 | 0.15 |
第二组(15≤x<30) | 6 | a |
第三组(30≤x<45) | 7 | 0.35 |
第四组(45≤x<60) | b | 0.20 |
(1)频数分布表中a=_____,b=_____,并将统计图补充完整;
(2)如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?
(3)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?