题目内容
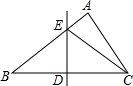
在Rt△ABC中，∠C=90°，BD平分∠ABC交AC于点D，DE垂直平分线段AB，
（1）试找出图中相等的线段，并说明理由．
（2）若DE=1cm，BD=2cm，求AC的长．
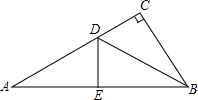
（1）试找出图中相等的线段，并说明理由．
（2）若DE=1cm，BD=2cm，求AC的长．
（1）图中相等的线段有AD=BD，CD=DE，BE=AE=BC，
理由是：∵DE垂直平分线段AB，
∴DE是线段AB的垂直平分线，
∴AD=BD，
∵∠C=90°，
∴DC⊥BC，
∵DE⊥BA，BD平分∠ABC，
∴CD=DE，
由勾股定理得：BE2=BD2-DE2，BC2=BD2-CD2，
∴BE=BC，
∵E为AB中点，
∴AE=BE=BC；
（2）∵由（1）知DE=DC=1cm，BD=AD=2CM，
∴AC=AD+DC=3cm．
理由是：∵DE垂直平分线段AB，
∴DE是线段AB的垂直平分线，
∴AD=BD，
∵∠C=90°，
∴DC⊥BC，
∵DE⊥BA，BD平分∠ABC，
∴CD=DE，
由勾股定理得：BE2=BD2-DE2，BC2=BD2-CD2，
∴BE=BC，
∵E为AB中点，
∴AE=BE=BC；
（2）∵由（1）知DE=DC=1cm，BD=AD=2CM，
∴AC=AD+DC=3cm．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
