题目内容
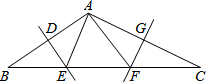
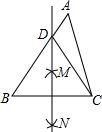
(1)已知:如图1,△ABC中,分别以AB、AC为一边向△ABC外作正方形ABGE和ACHF,直线AN⊥BC于N,若EP⊥AN于P,FQ⊥AN于Q.判断线段EP、FQ的数量关系,并证明;
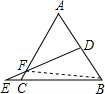
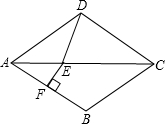
(2)如图2,梯形ABCD中,AD∥BC,分别以两腰AB、CD为一边向梯形ABCD外作正方形ABGE和DCHF,线段AD的垂直平分线交线段AD于点M,交BC于点N,若EP⊥MN于P,FQ⊥MN于Q.(1)中结论还成立吗?请说明理由.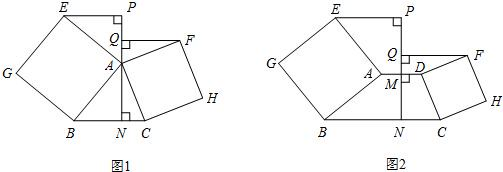
(2)如图2,梯形ABCD中,AD∥BC,分别以两腰AB、CD为一边向梯形ABCD外作正方形ABGE和DCHF,线段AD的垂直平分线交线段AD于点M,交BC于点N,若EP⊥MN于P,FQ⊥MN于Q.(1)中结论还成立吗?请说明理由.

(1)EP、FQ的数量关系是相等.
证明:∠QFA=90°-∠FAQ=∠CAN,
在△FQA与△ANC中,
,
∴△FQA≌△ANC(AAS),
∴FQ=AN;
同理△EPA≌△ANB,
∴EP=AN,
∴EP=FQ;
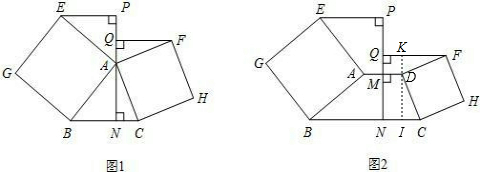
(2)答:(1)中的结论依然成立.理由如下:
过D作PN的平行线分别交FQ、BC于点K、I.
∵∠KFD=90°-∠FDK=∠CDI,
在△FKD与△DIC中,
∴△FKD≌△DIC(AAS),
∴FK=DI,
∴FQ=FK+KQ=DI+DM=DM+MN;
同理可得,EP=AM+MN,
又∵MN为AD中垂线,
∴AM=MD,
∴EP=AM+MN=DM+MN=FQ.
证明:∠QFA=90°-∠FAQ=∠CAN,
在△FQA与△ANC中,
|
∴△FQA≌△ANC(AAS),
∴FQ=AN;
同理△EPA≌△ANB,
∴EP=AN,
∴EP=FQ;

(2)答:(1)中的结论依然成立.理由如下:
过D作PN的平行线分别交FQ、BC于点K、I.
∵∠KFD=90°-∠FDK=∠CDI,
在△FKD与△DIC中,
|
∴△FKD≌△DIC(AAS),
∴FK=DI,
∴FQ=FK+KQ=DI+DM=DM+MN;
同理可得,EP=AM+MN,
又∵MN为AD中垂线,
∴AM=MD,
∴EP=AM+MN=DM+MN=FQ.

练习册系列答案
相关题目