题目内容
【题目】马山被誉为“中国民间文化艺术之乡”,马山的民族文化丰富多彩,形式多样.为了了解某学学生对马山民族文化的喜爱情况,某校开展了“我最喜爱的民俗活动”调查问卷,其中包括:![]() 壮族三声部民歌,
壮族三声部民歌,![]() 壮族扁担舞,
壮族扁担舞,![]() 会鼓,
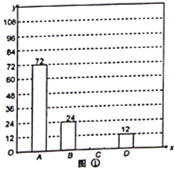
会鼓,![]() 采茶舞.将调查问卷结果收集整理后,绘制了以下不完整的条形统计图(图①)和扇形统计图(图②),根据图中所提供的信息解答下列问题:
采茶舞.将调查问卷结果收集整理后,绘制了以下不完整的条形统计图(图①)和扇形统计图(图②),根据图中所提供的信息解答下列问题:
(1)这次抽样调查中,一共抽查了名学生,![]() 项所对应圆心角的度数为;
项所对应圆心角的度数为;
(2)请补全条形统计图;
(3)若九(1)班要从甲、乙、丙和丁这四人中选两个人参与调查,请用列表法或画树状图法求出恰好选中甲乙的概率.

【答案】(1)120,![]() ;(2)见解析;(3)见解析,
;(2)见解析;(3)见解析,![]()
【解析】
(1)根据![]() 壮族三声部民歌的人数及所占的百分比计算总人数,进而计算
壮族三声部民歌的人数及所占的百分比计算总人数,进而计算![]() 项所对应圆心角的度数;
项所对应圆心角的度数;
(2)根据120×10%=12人,补全条形统计图即可;
(3)利用列表法或画树状图法列出所有的可能,再根据概率公式计算即可.
解:(1)72÷60%=120(人),
![]() 项所对应圆心角的度数为:
项所对应圆心角的度数为:![]() =36°
=36°
故答案为:120,![]() .
.
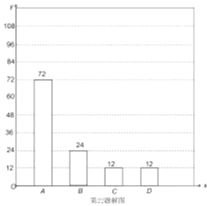
(2)补全条形统计图如图:
(3)列表如下:
甲 | 乙 | 丙 | 丁 | |
甲 | (乙,甲) | (丙,甲) | (丁,甲) | |
乙 | (甲,乙) | (丙,乙) | (丁,乙) | |
丙 | (甲,丙) | (乙,丙) | (丁,丙) | |
丁 | (甲,丁) | (乙,丁) | (丙,丁) |
或画树状图如下:
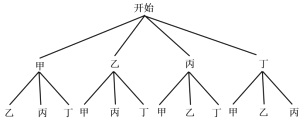
由列表(树状图)可知,共有12种等可能的结果,其中恰好选中甲乙的结果有2种.
∴![]() (恰好选中甲乙)
(恰好选中甲乙)![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】钟南山院士在谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷(满分100分),社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据
甲小区:80 85 90 95 90 95 90 65 75 100 90 70 95 90 80 80 90 95 60 100
乙小区:60 80 95 80 90 65 80 85 85 100 80 95 90 80 90 70 80 90 75 100
整理数据
成绩 小区 |
|
|
|
|
甲小区 |
|
|
|
|
乙小区 |
|
|
|
|
分析数据
数据名称 计量小区 | 平均数 | 中位数 | 众数 |
甲小区 |
|
|
|
乙小区 |
|
|
|
应用数据
(1)填空:![]() =______,
=______,![]() =______;
=______;
(2)若乙小区共有1200人参与答卷,请估计乙小区成绩大于90分的人数;
(3)社区管理人员看完统计数据,认为甲小区对新型冠状病毒肺炎防护知识掌握更好,请你写出社区管理人员的理由;为了更好地宣传新型冠状病毒肺炎防护知识,社区管理人员决定从甲、乙小区的4个满分试卷中随机抽取两份试卷对小区居民进行网络宣传讲解培训,请用列表格或画树状图的方法求出甲、乙小区各抽到一份满分试卷的概率.
【题目】某报社为了解温州市民对大范围雾霾天气的成因、影响以及应对措施的看法,做了一次抽样调查,调查结果共分为四个等级:A.非常了解:B.比较了解:C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.请结合统计图表,回答下列问题:
对雾霾的了解程度 | 百分比 | |
A | 非常了解 | 5% |
B | 比较了解 | m% |
C | 基本了解 | 45% |
D | 不了解 | n% |
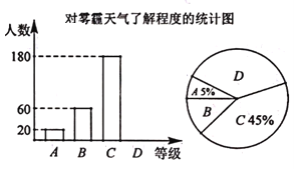
(1)本次参与调查的市民共有________人,m=________,n=________.
(2)统计图中扇形D的圆心角是________度.
(3)某校准备开展关于雾霾的知识竞赛,九(3)班郑老师欲从2名男生和1名女生中任选2人参加比赛,求恰好选中“1男1女”的概率(要求列表或画树状图).
【题目】某游泳馆推出了两种收费方式.
方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.
方式二:顾客不购买会员卡,每次游泳付费40元.
设小亮在一年内来此游泳馆游泳的次数为![]() 次(
次(![]() 为正整数).
为正整数).
(1)根据题意,填写下表:
游泳次数 | 5 | 10 | 15 | … |
|
方式一的总费用(元) | 350 | 650 | … | ||
方式二的总费用(元) | 200 | 400 | … |
(2)若小亮计划今年游泳的总费用为2000元,选择哪种付费方式,他游泳的次数比较多;
(3)当![]() 时,小亮选择哪种付费方式更合算.并说明理由.
时,小亮选择哪种付费方式更合算.并说明理由.