Question

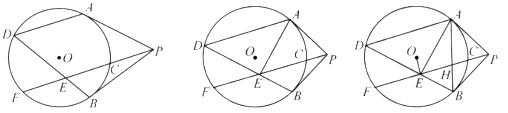
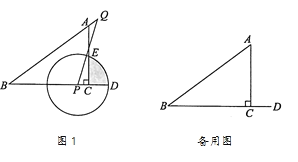
【题目】如图1，△ABC中，∠ACB=90°，AC=3，BC=4，延长BC到点D，使BD=BA，P是BC边上一点．点Q在射线BA上，PQ=BP，以点P为圆心，PD长为半径作⊙P，交AC于点E，连接PQ，设PC=x．

（1）AB=　　　　，CD=　　　　，当点Q在⊙P上时，求x的值；

（2）x为何值时，⊙P与AB相切？

（3）当PC=CD时，求阴影部分的面积；

（4）若⊙P与△ABC的三边有两个公共点，直接写出x的取值范围．

Answer 1

【答案】（1）5，1，x=；（2）x=；（3）－；（4）0≤x＜或＜x＜4．

【解析】

(1)先由勾股定理求得AB，再由BD=BA，可得BD的长，从而CD的长可求；当点Q在⊙P上时，如图1，根据PQ=PD推得BP=PD，从而列出方程，解得的值即可；
(2)作PF⊥AB于点F，当PF=PD时，⊙P与AB相切，如图2，由正弦函数得出关于 的方程，解得的值即可；
(3)如图3，连接PE，利用S阴影=S扇形PDE-S△PCE即可得出答案；
(4)由图1和图2即可得出答案．

(1)∵△ABC中，∠ACB=90°，AC=3，BC=4，
∴AB==5，
∵BD=BA，
∴BD=5，
∴CD= BD - BC=1．
故答案为：5，1；
当点Q在⊙P上时，如图1，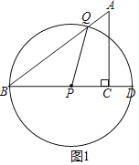

∵PQ=PD，BP= PQ，
∴BP=PD，
即．
解得：；

(2)作PF⊥AB于点F，当PF=PD时，⊙P与AB相切，如图2，

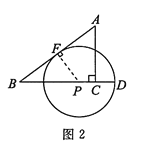
则PF=PD=x+1，

sinB==，

即=，

解得：x=，

经检验，x=是分式方程的解，且满足题意，

∴x=时，⊙P与AB相切；

(3)如图3，连接PE，

∵Rt△PEC中，PC=CD=1，PE=PD=1+1=2．

∵，

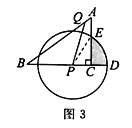
∴∠EPC=60°，EC==，

∴S阴影=S扇形PDE-S△PCE

=×1×

=-；

(4)由图2可知，当时，⊙P与△ABC的三边有两个公共点；

由图1可知，当时，⊙P与△ABC的三边有两个公共点．
∴的取值范围为：0≤x＜或＜x＜4．