Question

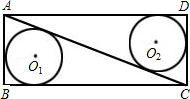
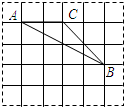
如图，△ABC中，∠C=90°，BC=4，AC=3，⊙O内切于△ABC，则阴影部分面积为（　　）

A．12-π

B．12-2π

C．14-4π

D．6-π

Answer 1

在Rt△ABC，∠C=90°，BC=3，AC=4；
根据勾股定理AB=

AC2+BC2

=5；
若设Rt△ABC的内切圆的半径为R，则有：
R=

AC+BC-AB

2

=1，
∴S_阴影=S_△ABC-S_圆
=

1

2

AC•BC-πR²
=

1

2

×3×4-π×1=6-π．
故选D．