Question

等腰三角形的底边长为2，面积等于1，则它的顶角度数为______．

Answer 1

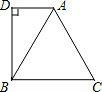
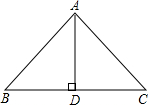
如图，设等腰△ABC的底边BC=2，
则

1

2

BC•AD=1，
即

1

2

×2•AD=1，
解得AD=1，
∵△ABC是等腰三角形，
∴BD=CD=

1

2

BC=1，
∴△ABD与△ACD都是等腰直角三角形，
∴∠BAD=∠CAD=45°，
∴∠BAC=45°×2=90°，
即它的顶角度数为90°．
故答案为：90°．