题目内容
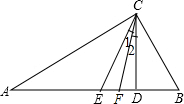
如图，△ABC中，∠BAC=90°，BC的垂直平分线和BC相交于点D，和∠BAC的平分线AE相交于点E，AE和BC相交于点F．求证：DE=
BC．
| 1 |
| 2 |
证明：连接AD．（1分）
∵∠BAC=90°，D是BC的中点，
∴DA=DC=
BC．（1分）
∴∠1=∠C．（1分）
又∵AE平分∠BAC，
∴∠CAF=45°．（1分）
∴∠2=45°-∠1．（1分）
又∵∠3=∠FAC+∠C
=45°+∠C，
∵DE⊥BC于点D，
∴∠E=90°-∠3
=90°-（45°+∠C）
=45°-∠C
∴∠2=∠E．
∴DE=AD．
∴DE=
BC．
∵∠BAC=90°，D是BC的中点，
∴DA=DC=
| 1 |
| 2 |
∴∠1=∠C．（1分）
又∵AE平分∠BAC，
∴∠CAF=45°．（1分）
∴∠2=45°-∠1．（1分）
又∵∠3=∠FAC+∠C
=45°+∠C，
∵DE⊥BC于点D，
∴∠E=90°-∠3
=90°-（45°+∠C）
=45°-∠C
∴∠2=∠E．
∴DE=AD．
∴DE=
| 1 |
| 2 |
练习册系列答案
相关题目
B、AC于点E、F，给出以下四个结论：
