��Ŀ����
����Ŀ����ͼ����¥AN������һ����AB��Сӱ������D�������������A������Ϊ30�㣬�����������ߵ��½�E����Ȼ�����¥�����������10������C������������ĵײ�B������Ϊ45�㣬��ʱСӱ���¥��N��20�ף���֪����DE=20�ף�ɽ�µ��¶�i=1�� ![]() ����tan��DEM=1��
����tan��DEM=1�� ![]() ������D��M��E��C��N��B��A��ͬһƽ���ڣ�E��C��N��ͬһ��ֱ���ϣ��������ij��ȣ������ȷ��1�ף����ο����ݣ�
������D��M��E��C��N��B��A��ͬһƽ���ڣ�E��C��N��ͬһ��ֱ���ϣ��������ij��ȣ������ȷ��1�ף����ο����ݣ� ![]() ��1.73��
��1.73�� ![]() ��1.41��
��1.41��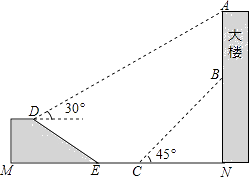
���𰸡��⣺����D��DH��AN��H������E��FE����DH��F��
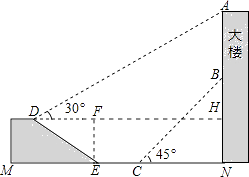
������DE=20�ף�ɽ�µ��¶�i=1�� ![]() ��
��
��EF=10�ף�DF=10 ![]() �ף�
�ף�
��DH=DF+EC+CN=��10 ![]() +30���ף���ADH=30�㣬
+30���ף���ADH=30�㣬
��AH= ![]() ��DH=��10+10
��DH=��10+10 ![]() ���ף�
���ף�
��AN=AH+EF=��20+10 ![]() ���ף�
���ף�
�ߡ�BCN=45�㣬
��CN=BN=20�ף�
��AB=AN��BN=10 ![]() ��17�ף�
��17�ף�
�������ij�����17�ף�
������������Ŀ�����˽�ֱ�������ε�Ӧ��.���AN��BN�ǹؼ�.����D��DH��AN��H������E��FE����DH��F�������¶Ⱥ�DE�����EF��DF����Rt��ADH�����AH��ֵ���Ӷ��ó�AN��ֵ����Rt��BCN�����BN��ֵ������AB=AN-BN�ɵ�.
�����㾫�����������⣬������Ҫ�˽��ֱ��������(��ֱ�������ε����ݣ��ٱߵĹ�ϵa2+b2=c2���ڽǵĹ�ϵ��A+B=90�㣻�۱߽ǹ�ϵ�����Ǻ����Ķ��壮(ע�⣺��������ʹ���м����ݺͳ���))����Ҫ���չ����¶��½�����(�����Ǧֱ�߶�h��ˮƽ����l�ıȽ����¶�(�±�)������ĸi��ʾ����i=h/l����������ˮƽ��ļнǼ���A(�����½�)����ôi=h/l=tanA)�����֪ʶ���Ǵ���Ĺؼ���

 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�