题目内容
【题目】如图所示,O是直线l上一点,在点O的正上方有一点A,满足OA=3,点A,B位于直线l的同侧,且点B到直线l的距离为5,线段AB=![]() ,一动点C在直线l上移动.
,一动点C在直线l上移动.
(1)当点C位于点O左侧时,且OC=4,直线l上是否存在一点P,使得△ACP为等腰三角形?若存在,请求出OP的长;若不存在,请说明理由.
(2)连结BC,在点C移动的过程中,是否存在一点C,使得AC+BC的值最小?若存在,请求出这个最小值;若不存在,请说明理由.


【答案】(1)存在,OP的长为4或1或9或![]() ;(2)存在,AC+BC的最小值为10.
;(2)存在,AC+BC的最小值为10.
【解析】
(1)存在,分三种情况分析即可: ①AP=CP, ②AP=AC, ③AC=PC;(2) 作点A关于直线l的对称点A′,根据两点之间线段最短即可求解.
(1)存在.由勾股定理可求得AC=5.当点P使得△ACP为等腰三角形时,
如图①所示,

OP1=4,OP2=5-4=1,OP3=CP3+OC=AC+OC=5+4=9.
在Rt△AP4O中,AP42=OP42+OA2,
设OP4=x,则(4-x)2=x2+32,
解得x=![]() ,∴OP4=
,∴OP4=![]() .
.
综上所述,OP的长为4或1或9或![]() .
.
(2)存在.如图②所示,作点A关于直线l的对称点A′,连结A′B与直线l相交于点C,
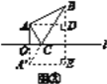
则A′B为AC+BC的最小值.
过点A′作A′E∥l,过点B作BE⊥A′E于点E,过点A作AD⊥BE于点D.
在Rt△ABD中,AB=![]() ,BD=5-3=2,
,BD=5-3=2,
∴AD=![]() =6.
=6.
在Rt△A′BE中,A′E=AD=6,BE=5+3=8,
∴A′B=![]() =10,
=10,
∴AC+BC的最小值为10.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目