Question

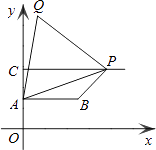
【题目】如图，在平面直角坐标系中，△ABC是等腰直角三角形，∠BAC=90°，A（1，0），B（0，2），C（3，1）抛物线y= x2+bx﹣2的图象过C点，交y轴于点D．

（1）在后面的横线上直接写出点D的坐标及b的值： ， b=；
（2）平移该抛物线的对称轴所在直线l，设l与x轴交于点G（x，0），当OG等于多少时，恰好将△ABC的面积分为相等的两部分？
（3）点P是抛物线上一动点，是否存在点P，使四边形PACB为平行四边形？若存在，直接写出P点坐标；若不存在，说明理由．

Answer 1

【答案】
（1）（0，﹣2）；
（2）

解：在Rt△A0B中，OA=1，OB=2，由勾股定理，得

AB2=OA2+OB2=5，

∴S△ABC= AB2= ，

设l与AC、BC分别交于E，F，直线BC所在的直线解析式为y=kx+b，

将B（0，2），C（3，1）代入函数解析式，得

，

解得 ，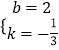

直线BC的解析式为y=﹣ x+2，

同理直线AC的解析式为y= x﹣ ，

∴点E，F的坐标为E（x， x﹣ ），F（x，﹣ x+2），

EF=（﹣ x+2）﹣（ x﹣ ）= ﹣ x，

过C作CH⊥x轴于H点，

在△CEF中，EF边上的高h=OH﹣x=3﹣x，

由题意可知S△CEF= S△ABC= EFh，

即 （ ﹣ x）（3﹣x）= × ，

解得x1=3﹣ ，x2=3+ （不符合题意，舍），

当OG=3﹣ 时，恰好将△ABC的面积分为相等的两部分；

（3）

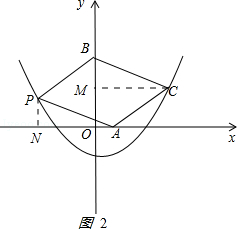
解：抛物线上存在点P，使四边形PACB为平行四边形，

如图2

，

过C作CM⊥y轴于点M，则CM=3，OM=1，BM=OB﹣OM=1．

过点P作PA∥BC，且AP=BC，连接BP，则四边形PABC是平行四边形，

∵ ，

∴∠PAN=∠BCM．

过点P作PN⊥x轴于N，

在△APN和△CBM中，

∴△PAN≌△BCM，

∴PN=BM=1，AN=CM=3，

∴ON=AN﹣OA=2，

∴P点坐标为（﹣2，1）．

抛物线解析式为：y= x2+ x﹣2，当x=﹣2时，y=1，即点P在抛物线上．

∴存在符合条件的点P，点P的坐标为（﹣2，1）．

【解析】解：（1）将C点坐标代入解析式，得 ×32+3b﹣2=1，解得b= ，函数解析式y= x2+ x﹣2，当x=0时，y=﹣2，即D（0，﹣2），所以答案是：（0，﹣2）， ；
【考点精析】本题主要考查了确定一次函数的表达式和勾股定理的概念的相关知识点，需要掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题．