题目内容
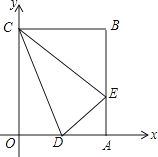
【题目】如图,已知点A(0,2)、B(2 ![]() ,2)、C(0,4),过点C向右做平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在左侧作等边△APQ,连接PB、BA.
,2)、C(0,4),过点C向右做平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在左侧作等边△APQ,连接PB、BA. 
(1)当AB∥PQ时,点P的横坐标是;
(2)当BP∥QA时,点P的横坐标是 .
【答案】
(1)![]()
(2)0或2 ![]()
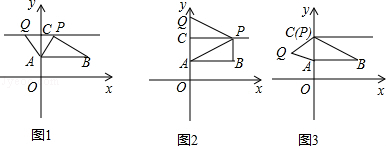
【解析】解:(1)如图1:当AB为梯形的底时,PQ∥AB, ∴Q在CP上,
∵△APQ是等边三角形,CP∥x轴,
∴AC垂直平分PQ,
∵A(0,2),C(0,4),
∴AC=2,
∴PC=ACtan30°=2× ![]() =
= ![]() ,
,
∴当AB为梯形的底时,点P的横坐标是: ![]() ;
;
⑵如图2,当AB为梯形的腰时,AQ∥BP,
∴Q在y轴上,
∴BP∥y轴,
∵CP∥x轴,
∴四边形ABPC是平行四边形,
∴CP=AB=2 ![]() ,
,
如图3,当C与P重合时,
∵A(0,2)、B(2 ![]() ,2),
,2),
∴tan∠APB= ![]() =
= ![]() ,
,
∴∠APB=60°,
∵△APQ是等边三角形,
∴∠PAQ=60°,
∴∠ACB=∠PAQ,
∴AQ∥BP,
∴当C与P重合时,四边形ABPQ以AB为腰的梯形,
此时点P的横坐标为0;
∴当AB为梯形的腰时,点P的横坐标是:0或2 ![]() .
.
所以答案是:(1) ![]() ;(2)0或2
;(2)0或2 ![]() .
.
【考点精析】本题主要考查了等边三角形的性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.

练习册系列答案
相关题目