题目内容
【题目】如图1,点P(m,n)在一次函数![]() 的图像上,将点P绕点A(
的图像上,将点P绕点A(![]()
![]() ,
,![]() )逆时针旋转45°,旋转后的对应点为P.
)逆时针旋转45°,旋转后的对应点为P.
(1)当![]() 时,求点P的坐标;
时,求点P的坐标;
(2)试说明:不论m为何值,点P的纵坐标始终不变;
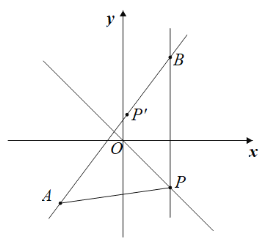
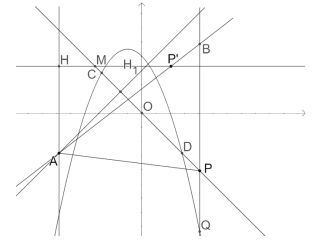
(3)如图2,过点P作x轴的垂线交直线AP于点B,若直线PB与二次函数![]() 的图像交于点Q,当m>0时,试判断点B是否一定在点Q的上方,请说明理由.
的图像交于点Q,当m>0时,试判断点B是否一定在点Q的上方,请说明理由.
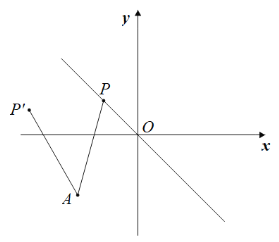
【答案】(1)![]() ;(2)理由见解析;(3)点 B一定在点Q的上方,理由见解析
;(2)理由见解析;(3)点 B一定在点Q的上方,理由见解析
【解析】
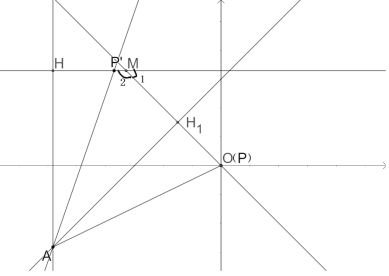
(1)如图 当m=0时,P与O重合,过A作![]() ⊥直线y=-x,过
⊥直线y=-x,过![]() 作直线
作直线![]() ∥x轴,交直线y=-x于M点,过A作AH⊥
∥x轴,交直线y=-x于M点,过A作AH⊥![]() 于H,可以求出直线
于H,可以求出直线![]() 的解析式,进而求出
的解析式,进而求出![]() ,由长度公式可得
,由长度公式可得![]() ,证明
,证明![]() 即可求出答案;
即可求出答案;
(2)无论m<0,m=0,m>0时,均有![]() 故
故![]() 故可得出:
故可得出:![]() 点的纵坐标;
点的纵坐标;
(3)求出![]() 与
与![]() 的交点,分P在交点的左右两侧及交点上进行画图,由图像即可得出:点 B一定在点Q的上方.
的交点,分P在交点的左右两侧及交点上进行画图,由图像即可得出:点 B一定在点Q的上方.
(1)如图 当m=0时,P与O重合
过A作![]() ⊥直线y=-x
⊥直线y=-x
故设直线![]() 的解析式为
的解析式为![]()
把![]() 代入
代入![]() 可得
可得
![]()
所以![]()
∴![]()
∵
∴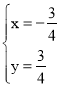
∴![]()
∵![]()
由长度公式可得![]()
∵y=-x
∴∠1=45°
∴∠2=180°-45°=135°
过![]() 作直线
作直线![]() ∥x轴,交直线y=-x于M点,过A作AH⊥
∥x轴,交直线y=-x于M点,过A作AH⊥![]() 于H
于H
∴∠AHP=![]() =90°
=90°
∴在四边形![]() 中:
中:![]()
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∵![]()
∴H点的纵坐标为:![]()
∴![]()
∴![]() 的横坐标为:
的横坐标为:![]()
∴![]()
 ;
;
(2)当m<0,m=0,m>0时,点P 的纵坐标均为![]() ,证明过程如下:
,证明过程如下:
当m<0,m=0,m>0时,均有:
∵y=-x
∴∠1=45°
∴∠2=180°-45°=135°
过![]() 作直线
作直线![]() ∥x轴,交直线y=-x于M点,过A作AH⊥
∥x轴,交直线y=-x于M点,过A作AH⊥![]() 于H
于H
∴∠AHP=![]() =90°
=90°
∴在四边形![]() 中:
中:![]()
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]()
故![]()
![]()
∴![]() 点的纵坐标为:
点的纵坐标为:![]()
故:当m<0,m=0,m>0时,点P 的纵坐标均为![]()
(3)点 B一定在点Q的上方,理由如下:
∵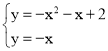
解得: 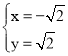 或
或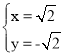
∴![]() 与
与 ![]() 交于C
交于C![]() ,D
,D![]() 两点
两点
∴由图像可知当![]() 时
时
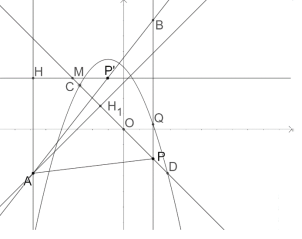
∠QAP<45°,∠BAP=45°
故B在Q的上方
当![]() 时,由图像可知:P、Q、D三点重合
时,由图像可知:P、Q、D三点重合
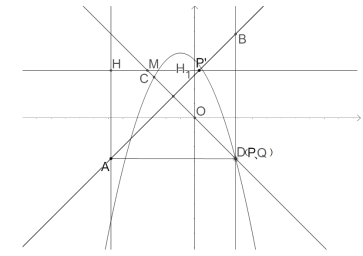
点 B一定在点Q的上方
当![]() 时,由图像可知:
时,由图像可知:
Q在直线y=-x的下方B在直线y=-x的上方
∴B在Q的上方
综上所述:当m>0时,点 B一定在点Q的上方

【题目】甲、乙两校各选派10名学生参加“美丽泰州乡土风情知识”大赛预赛.各参赛选手的成绩如下:
甲校:93,98,89,93, 95,96, 93,96,98, 99;
乙校:93,94,88,91,92,93,100, 98,98,93.
通过整理,得到数据分析表如下:
学校 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
甲校 | 99 | a | 95.5 | 93 | 8.4 |
乙校 | 100 | 94 | b | 93 | c |
(1)填空:a = ,b = ;
(2)求出表中c的值,你认为哪所学校代表队成绩好?请写出两条你认为该队成绩好的理由.
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的