题目内容
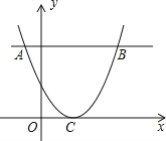
【题目】如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.
(1)求证:AC是⊙O的切线:
(2)若BF=8,DF=![]() ,求⊙O的半径;
,求⊙O的半径;
(3)若∠ADB=60°,BD=1,求阴影部分的面积.(结果保留根号)

【答案】(1)证明见解析;(2)6;(3)![]() .
.
【解析】
(1)连接OA、OD,如图,利用垂径定理的推论得到OD⊥BE,再利用CA=CF得到
∠CAF= ∠CFA,然后利用角度的代换可证明∠OAD+∠CAF=![]() ,则OA⊥AC,从而根据
,则OA⊥AC,从而根据
切线的判定定理得到结论;
(2)设⊙0的半径为r,则OF=8-r,在Rt△ODF中利用勾股定理得到
![]() ,然后解方程即可;
,然后解方程即可;
(3)先证明△BOD为等腰直角三角形得到OB=![]() ,则OA=
,则OA=![]() ,再利用圆周角定理得到∠AOB=2∠ADB=
,再利用圆周角定理得到∠AOB=2∠ADB=![]() ,则∠AOE=
,则∠AOE=![]() ,接着在Rt△OAC中计算出AC,然后用一个直角三角形的面积减去一个扇形的面积去计算阴影部分的面积.
,接着在Rt△OAC中计算出AC,然后用一个直角三角形的面积减去一个扇形的面积去计算阴影部分的面积.
(1)证明:连接OA、OD,如图,
∵D为BE的下半圆弧的中点,
∴OD⊥BE,
∴∠ODF+∠OFD=90°,
∵CA=CF,
∴∠CAF=∠CFA,
而∠CFA=∠OFD,
∴∠ODF+∠CAF=90°,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠OAD+∠CAF=90°,即∠OAC=90°,
∴OA⊥AC,
∴AC是⊙O的切线;
(2)解:设⊙O的半径为r,则OF=8﹣r,
在Rt△ODF中,(8﹣r)2+r2=(![]() )2,解得r1=6,r2=2(舍去),
)2,解得r1=6,r2=2(舍去),
即⊙O的半径为6;
(3)解:∵∠BOD=90°,OB=OD,
∴△BOD为等腰直角三角形,
∴OB=![]() BD=
BD=![]() ,
,
∴OA=![]() ,
,
∵∠AOB=2∠ADB=120°,
∴∠AOE=60°,
在Rt△OAC中,AC=![]() OA=
OA=![]() ,
,
∴阴影部分的面积=![]()
![]()
![]() ﹣
﹣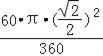 =
=![]() .
.