题目内容
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数y= ![]() 交于C、D两点.已知点C坐标为(﹣4,﹣1),点D的横坐标为2.
交于C、D两点.已知点C坐标为(﹣4,﹣1),点D的横坐标为2.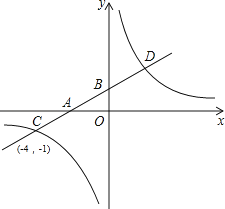
(1)求反比例函数与一次函数的解析式;
(2)若点P为坐标轴上一点,且S△ACP=2S△ABO , 请直接写出点P的坐标.
【答案】
(1)
解:∵点C坐标为(﹣4,﹣1)在反比例函数y= ![]() 的图象上,
的图象上,
∴﹣1= ![]() ,
,
解得:n=4,
∴反比例函数的解析式为:y= ![]() ;
;
∵点D的横坐标为2,
∴y= ![]() =2,
=2,
∴点D(2,2),
将点C与D代入一次函数解析式,可得: ![]() ,
,
解得: ![]() ,
,
∴一次函数的解析式的解析式为:y= ![]() x+1;
x+1;
(2)
解:如图

∵一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,
∴A(﹣2,0),B(0,1),
∴S△ABO= ![]() ×2×1=1,
×2×1=1,
∴S△ACP=2S△ABO=2,
若点P在x轴上,则AP=4,
∴点P的坐标为:(﹣6,0)或(2,0),
若点P在y轴上,则S△ACP=S△BCP﹣S△ABP= ![]() ×4×BP﹣
×4×BP﹣ ![]() ×BP×2=2,
×BP×2=2,
∴BP=2,
∴点P(0,3)或(0,﹣1).
综上可得:点P的坐标为:(﹣6,0),(2,0),(0,3)或(0,﹣1).
【解析】(1)由一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数y= ![]() 交于C、D两点.已知点C坐标为(﹣4,﹣1),点D的横坐标为2,利用待定系数法即可求得反比例函数与一次函数的解析式;(2)分别从点P在x轴上与在y轴上,去分析求解即可求得答案.
交于C、D两点.已知点C坐标为(﹣4,﹣1),点D的横坐标为2,利用待定系数法即可求得反比例函数与一次函数的解析式;(2)分别从点P在x轴上与在y轴上,去分析求解即可求得答案.

【题目】小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
通话时间x/分钟 | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 |
频数(通话次数) | 20 | 16 | 9 | 5 |
则5月份通话次数中,通话时间不超过15分钟的所占百分比是( )
A. 10% B. 40% C. 50% D. 90%