题目内容
【题目】如图所示,两个建筑物AB和CD的水平距离为30m,张明同学住在建筑物AB内10楼P室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.( ![]() 取1.73,结果保留整数.)
取1.73,结果保留整数.)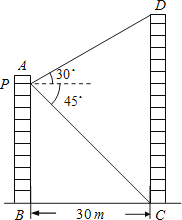
【答案】解:过点P作PE⊥CD于E,则四边形BCEP是矩形.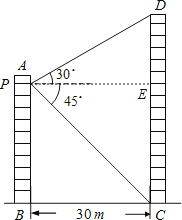
∴PE=BC=30.
在Rt△PDE中,∵∠DPE=30°,PE=30,
∴DE=PE×tan30°=30× ![]() =10
=10 ![]() .
.
在Rt△PEC中,∵∠EPC=45°,PE=30,
∴CE=PE×tan45°=30×1=30.
∴CD=DE﹢CE=30﹢10 ![]() =30﹢17.3≈47(m)
=30﹢17.3≈47(m)
答:建筑物CD的高约为47 m.
【解析】过点P作PE⊥CD于E,则四边形BCEP是矩形,得到PE=BC=30,在Rt△PDE中,利用∠DPE=30°,PE=30,求得DE的长;在Rt△PEC中,利用∠EPC=45°,PE=30求得CE的长,利用CD=DE﹢CE即可求得结果.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目