题目内容
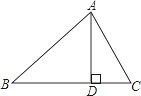
【题目】已知:如图,△ABC中,AD⊥BC,点D为垂足,AD=BD,点E在AD上,BE=AC
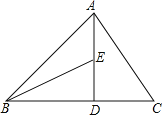
(1)求证:△BDE≌△ADC
(2)若M、N分别是BE、AC的中点,分别联结DM、DN. 求证:DM⊥DN
【答案】(1)见解析;(2)见解析
【解析】
(1)运用HL证明△BDE≌△ADC即可;
(2)由△BDE≌△ADC可得DE=DC,∠DEM=∠C,BE=AC,再依据M、N分别是BE、AC的中点,从而可得CN=EM,进而可证明△DEM≌△DCN,可得∠CDN=∠EDM,结合∠ADC=90°即可证得结论.
(1)∵AD⊥BC,
∴∠ADC=∠BDE=90°,
在Rt△ADC和Rt△BDE中,
![]()
∴△BDE≌△ADC;
(2)如图,
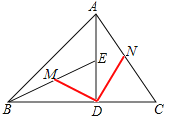
∵△BDE≌△ADC,
∴DE=DC,∠DEM=∠C,
∵M、N分别是BE、AC的中点且BE=AC,
∴EM=CN,
在△DEM和△DCN中,
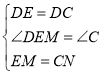
∴△DEM≌△DCN
∴∠EDM=∠CDN
∵∠CDN+∠NDA=90°,
∴∠MDA+∠NDA=90°,
即DM⊥DN.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目