题目内容
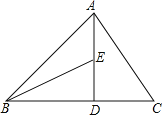
【题目】如图,已知△ABC中,∠ABC=50°,P为△ABC内一点,过点P的直线MN分別交AB、BC于点M、N.若M在PA的中垂线上,N在PC的中垂线上,则∠APC的度数为____________°

【答案】115°
【解析】
根据三角形的内角和得到∠BAC+∠ACB=130°,根据线段的垂直平分线的性质得到AM=PM,PN=CN,由等腰三角形的性质得到∠MAP=∠APM,∠CPN=∠PCN,推出∠MAP+∠PCN=∠PAC+∠ACP=![]() ×130°=65°,于是得到结论.
×130°=65°,于是得到结论.
∵∠ABC=50°,
∴∠BAC+∠ACB=130°,
∵若M在PA的中垂线上,N在PC的中垂线上,
∴AM=PM,PN=CN,
∴∠MAP=∠APM,∠CPN=∠PCN,
∵∠APC=180°-∠APM-∠CPN=180°-∠PAC-∠ACP,
∴∠MAP+∠PCN=∠PAC+∠ACP=![]() ×130°=65°,
×130°=65°,
∴∠APC=115°,
故答案为:115°

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为考察两名实习工人的工作情况,质检部将他们工作某一周每天生产合格产品的个数整理成甲、乙两组数据,如下表:
甲 | 2 | 6 | 7 | 7 | 8 |
乙 | 2 | 4 | 5 | 8 | 8 |
根据以上数据,下面说法正确的是( )
A.甲、乙的众数相同B.甲、乙的中位数相同
C.甲的平均数小于乙的平均数D.甲的方差小于乙的方差