题目内容
【题目】数学课上,王老师出示了如下框中的题目.

小明与同桌小聪讨论后,进行了如下解答:
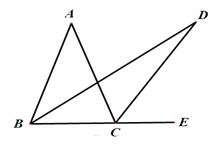
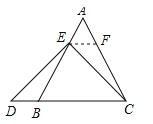
(1)特殊情况探索结论:在等边三角形ABC中,当点E为AB的中点时,点D在CB点延长线上,且ED=EC;如图1,确定线段AE与DB的大小关系.请你直接写出结论 ;
(2)特例启发,解答题目
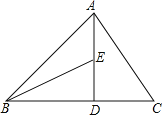
王老师给出的题目中,AE与DB的大小关系是: .理由如下:
如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
(3)拓展结论,设计新题
在△ABC中,AB=BC=AC=1;点E在AB的延长线上,AE=2;点D在CB的延长线上,ED=EC,如图3,请直接写CD的长 .
【答案】(1)![]() ;(2)
;(2)![]() ,见详解;(3)3.
,见详解;(3)3.
【解析】
(1)根据等边三角形三线合一的性质可知BE=AE,利用角的度数证明![]() ,可得
,可得![]() ,等量代换即可;
,等量代换即可;
(2)过点E作EF∥BC交AC于点F,利用AAS证![]() 即可得结论;
即可得结论;
(3)作EF∥BC交AC的延长线于点F,利用等边三角形及平行线的性质易证![]() ,可得BD长,CD长可知.
,可得BD长,CD长可知.
解:(1)![]() 是等边三角形
是等边三角形
![]()
![]() 点E为AB的中点
点E为AB的中点
![]() 是
是![]() 的角平分线
的角平分线
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(2)![]()
如图,过点E作EF∥BC交AC于点F
![]()
![]() 是等边三角形,
是等边三角形,![]()
![]()
又![]()
![]()
![]()
![]()
又![]()
![]()
在![]() 和
和![]() 中
中
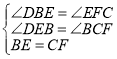
![]()
![]()
![]()
(3)作EF∥BC交AC的延长线于点F
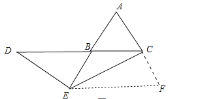
![]() 是等边三角形
是等边三角形
![]()
![]()
![]()
![]()
![]() ,且AE=AF=EF
,且AE=AF=EF
![]()
![]()
![]()
![]()
![]()
![]()

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目